Арифметика

В математике было бы мало пользы, если бы она остановилась после создания одной сущности; это действие можно повторить. Мы снова можем задать философские вопросы: как возможно, что сущность, которая была создана, сохраняет свою индивидуальность, и как возможно отличить ее от другой сущности?

Но это снова рассуждение post factum: каждый может обнаружить, что он способен сконцентрировать внимание на одном восприятии, затем на другом, сохраняя первое в своей памяти. Это образует основу счета. Не имеет значения, что пересчитывается, но важен сам процесс счета, сама деятельность ума. Создавая сущность, другую, еще одну, и т.д., мы конструируем в уме натуральные числа. Ясно, что при построении, скажем, натурального числа 5 природа сущностей, образующих это число, абсолютно безразлична. Когда появились цифры, люди научились абстрагироваться от содержания изолированных восприятий и рассматривать их как чистые сущности. Мы построили каждое натуральное число отдельно. Пока мы не в состоянии делать высказывания о всяком натуральном числе. Обычно такие высказывания формулируются при помощи квантора общности: для каждого натурального числа $n$ выполняется $A(n)$. Но лучше сформулировать это так: пусть $n$ натуральное число, тогда выполняется $A(n)$. Или более явно: допустим, мы построили натуральное число $n$, тогда мы можем доказать $A(n)$. Видно, что здесь содержится понятие гипотетического построения. Оно является фундаментальным в математике. Почти любую теорему можно привести к виду: допустим, что проведено построение $A$, тогда мы можем также провести построение $B$. Доказательство такой теоремы состоит в построении, которое, будучи соединено с построением $A$, даст построение $B$.

Позвольте мне привести пример. Я хочу доказать теорему: если $n$ произвольное натуральное число, то существует простое число, большее $n$. Доказательство: вычислить $n!+1$; разложить это число на множители; каждый из простых делителей будет больше $n$. Представленное доказательство состоит в общем методе построения, применимом к гипотетическому построению.

До сих пор мы использовали понятия натурального числа, гипотетического построения натурального числа, общего метода построения, применяемого к гипотетической конструкции.

Этих понятий достаточно для арифметики. Рассмотрим отдельно принцип полной индукции:

$$A(1) \land \forall x (A(x) \to A(x+1)) \to \forall x A(x).$$

Допустим, что мы доказали $A(0)$, и у нас есть общий метод $M$, позволяющий для всякого натурального числа $x$ вывести доказательство $A(x+1)$ из гипотетического доказательства $A(x)$. Пусть $n$ — произвольное натуральное число. Для того, чтобы доказать $A(n)$, мы строим число $n$ и на каждом шаге от $x$ к $x+1$ применяем $M$, чтобы получить $A(x+1)$. Результатом будет доказательство $A(n)$.

Я хочу предостеречь от ошибочного представления, что нам требуется общий принцип полной индукции; все, что действительно нужно — это применение в каждом конкретном случае; и каждый раз оно очевидно.

Например, я хочу доказать, что $\sum_1^n k = n(n+1)/2$. Это верно для $n=1$.

Допустим, это доказано для $x$ (гипотетическое построение).

$$\sum_1^{x+1}k = \frac{x(x+1)}{2}+x+1 = \frac{(x+1)(x+2)}{2} \qquad \hbox{(общий метод).}$$

Пусть $n$ — произвольное натуральное число. Я могу доказать $A(x)$ последовательно для $x=1,\ldots,n$. Последнее есть прямое применение определения к натуральному числу.

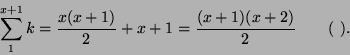
Можно обосновать, что никакие другие понятия, за исключением упомянутых, в арифметике не требуются. Арифметические суждения образуются из простейших отношений $a=b$ и $a<b$ посредством связок $\land$, $\lor$, $\to$, $\lnot$ и кванторов $\forall$, $\exists$. Доказательство $a=b$ состоит в одновременном построении $a$ и $b$ таким образом, что когда некоторая сущность добавляется к $a$, то же самое делается и с $b$. Аналогичное объяснение можно дать и для $a<b$. Конечно, логические константы надо интерпретировать в терминах построений. Я вернусь к этому позднее; пока будет полезно сделать несколько замечаний. Интерпретация $A \to B$ уже неявно упоминалась: доказательство $A \to B$ состоит в общем методе, перестраивающем каждое доказательство $A$ в доказательство $B$. Доказательство $\lnot A$ состоит в методе, который мог бы перевести предполагаемое доказательство $A$ в противоречие. Я склонен считать, что это определение необходимо принять за основу. Мы ясно понимаем невозможность $1=2$, но это понятие не сводится к другим, которые я упоминал. Имеет смысл избегать использования отрицания, когда это возможно. Работа Бишопа показывает, что наиболее важные разделы анализа могут быть построены положительно ([1]).

Доказательство $\forall x A(x)$ состоит в общем методе, переводящем построение натурального числа $x$ в доказательство $A(x)$.

Наконец, доказательство $\exists x A(x)$ есть комбинация построения натурального числа $x$ и доказательства $A(x)$.

Единственное фундаментальное понятие, возникающее здесь, — понятие противоречия.