Epsilon Calculi are extended forms of
the predicate calculus that incorporate epsilon terms. Epsilon
terms are individual terms of the form ' xFx', being defined for all predicates in the
language. The epsilon term ' xFx', being defined for all predicates in the
language. The epsilon term ' xFx' denotes a chosen F, if there are any F's,
and has an arbitrary reference otherwise. Epsilon calculi were
originally developed to study certain forms of Arithmetic, and
Set Theory; also to prove some important meta-theorems about
the predicate calculus. Later formal developments have
included a variety of intensional epsilon calculi, of use in
the study of necessity, and more general intensional notions,
like belief. An epsilon term such as ' xFx' denotes a chosen F, if there are any F's,
and has an arbitrary reference otherwise. Epsilon calculi were
originally developed to study certain forms of Arithmetic, and
Set Theory; also to prove some important meta-theorems about
the predicate calculus. Later formal developments have
included a variety of intensional epsilon calculi, of use in
the study of necessity, and more general intensional notions,
like belief. An epsilon term such as ' xFx' was originally read 'the first F', and in
arithmetical contexts 'the least F'. More generally it can be
read as the demonstrative description 'that F', when arising
either deictically, i.e. in a pragmatic context where some F
is being pointed at, or in linguistic cross-reference
situations, as with, for example, 'There is a red haired man
in the room. That red haired man is Caucasian'. The
application of epsilon terms to natural language shares some
features with the use of iota terms within the theory of
descriptions given by Bertrand Russell, but differs in
formalising aspects of a slightly different theory of
reference, first given by Keith Donnellan. More recently
epsilon terms have been used by a number of writers to
formalise cross-sentential anaphora, which would arise if
'that red haired man' in the linguistic case above was
replaced with a pronoun such as 'he'. There is then also the
similar application in intensional cases, like 'There is a red
haired man in the room. Celia believed he was a
woman.' xFx' was originally read 'the first F', and in
arithmetical contexts 'the least F'. More generally it can be
read as the demonstrative description 'that F', when arising
either deictically, i.e. in a pragmatic context where some F
is being pointed at, or in linguistic cross-reference
situations, as with, for example, 'There is a red haired man
in the room. That red haired man is Caucasian'. The
application of epsilon terms to natural language shares some
features with the use of iota terms within the theory of
descriptions given by Bertrand Russell, but differs in
formalising aspects of a slightly different theory of
reference, first given by Keith Donnellan. More recently
epsilon terms have been used by a number of writers to
formalise cross-sentential anaphora, which would arise if
'that red haired man' in the linguistic case above was
replaced with a pronoun such as 'he'. There is then also the
similar application in intensional cases, like 'There is a red
haired man in the room. Celia believed he was a
woman.'
Table of Contents
(Clicking on the links below will take you to those parts of
this article)
1.
Introduction
Epsilon terms were introduced by the german mathematician
David Hilbert, in Hilbert 1923, 1925, to provide explicit
definitions of the existential and universal quantifiers, and
resolve some problems in infinitistic mathematics. But it is
not just the related formal results, and structures which are
of interest. In Hilbert's major book Grundlagen der
Mathematik, which he wrote with his collaborator Paul
Bernays, epsilon terms were presented as formalising certain
natural language constructions, like definite descriptions.
And they in fact have a considerably larger range of such
applications, for instance in the symbolisation of certain
cross-sentential anaphora. Hilbert and Bernays also used their
epsilon calculus to prove two important meta-theorems about
the predicate calculus. One theorem subsequently led, for
instance, to the development of semantic tableaux: it is
called the First Epsilon Theorem, and its content and proof
will be given later, in section
6 below. A second theorem that Hilbert and Bernays proved,
which we shall also look at then, establishes that epsilon
calculi are conservative extensions of the predicate calculus,
i.e. that no more theorems expressible just in the
quantificational language of the predicate calculus can be
proved in epsilon calculi than can be proved in the predicate
calculus itself. But while epsilon calculi do have these
further important formal functions, we will not only be
concerned to explore them, for we shall also first discuss the
natural language structures upon which epsilon calculi have a
considerable bearing.
The growing awareness of the larger meaning and
significance of epsilon calculi has only come in stages.
Hilbert and Bernays introduced epsilon terms for several
meta-mathematical purposes, as above, but the extended
presentation of an epsilon calculus, as a formal logic of
interest in its own right, in fact only first appeared in
Bourbaki's ╔lķments de Mathķmatique (although see also
Ackermann 1937-8). Bourbaki's epsilon calculus with identity
(Bourbaki, 1954, Book 1) is axiomatic, with Modus Ponens as
the only primitive inference or derivation rule. Thus, in
effect, we get:
(X v X)
 X, X,
X  (X v Y), (X v Y),
(X v Y)  (Y v X), (Y v X),
(X v Y)  ((Z v X) ((Z v X)  (Z v Y)), (Z v Y)),
Fy  F F xFx, xFx,
x = y  (Fx (Fx  Fy), Fy),
(x)(Fx  Gx) Gx)   xFx = xFx =  xGx. xGx.
This adds to a basis for the propositional calculus an
epsilon axiom schema, then Leibniz' Law, and a second epsilon
axiom schema, which is a further law of identity. Bourbaki,
though, used the Greek letter tau rather than epsilon to form
what are now called 'epsilon terms'; nevertheless, he defined
the quantifiers in terms of his tau symbol in the manner of
Hilbert and Bernays, viz:
( x)Fx x)Fx  F F xFx, xFx,
(x)Fx  F F x¼Fx; x¼Fx;
and note that, in his system the other usual law of
identity, 'x = x', is derivable.
The principle purpose Bourbaki found for his system of
logic was in his theory of sets, although through that, in the
modern manner, it thereby came to be the foundation for the
rest of mathematics. Bourbaki's theory of sets discriminates
amongst predicates those which determine sets: thus some, but
only some, predicates determine sets, i.e. are
'collectivisantes'. All the main axioms of classical Set
Theory are incorporated in his theory, but he does not have an
Axiom of Choice as a separate axiom, since its functions are
taken over by his tau symbol. The same point holds in Bernays'
epsilon version of his set theory (Bernays 1958, Ch VIII).
Epsilon calculi, during this period, were developed without
any semantics, but a semantic interpretation was produced by
Gunter Asser in 1957, and subsequently published in a book by
A.C. Leisenring, in 1969. Even then, readings of epsilon terms
in ordinary language were still uncommon. A natural language
reading of epsilon terms, however, was present in Hilbert and
Bernays' work. In fact the last chapter of book 1 of the
Grundlagen is a presentation of a theory of definite
descriptions, and epsilon terms relate closely to this. In the
more well known theory of definite descriptions by Bertrand
Russell (Russell 1905) there are three clauses: with
The king of France is bald
we get, on Russell's theory, first
there is a king of France,
second
there is only one king of France,
and third
anyone who is king of France is bald.
Russell uses the Greek letter iota to formalise the
definite description, writing the whole
B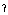 xKx, xKx,
but he recognises the iota term is not a proper individual
symbol. He calls it an 'incomplete symbol', since, because of
the three parts, the whole proposition is taken to have the
quantificational analysis,
( x)(Kx & (y)(Ky x)(Kx & (y)(Ky  y = x) & (y)(Ky y = x) & (y)(Ky  By)), By)),
which is equivalent to
( x)(Kx & (y)(Ky x)(Kx & (y)(Ky y = x) & Bx). y = x) & Bx).
And that means that it does not have the form 'Bx'. Russell
believed that, in addition to his iota terms, there was
another class of individual terms, which he called 'logically
proper names'. These would simply fit into the 'x' place in
'Bx'. He believed that 'this' and 'that' were in this class,
but gave no symbolic characterisation of them.
Hilbert and Bernays, by contrast, produced what is called a
'pre-suppositional theory' of definite descriptions. The first
two clauses of Russell's definition were not taken to be part
of the meaning of 'The King of France is bald': they were
merely conditions under which they took it to be permitted to
introduce a complete individual term for 'the King of France',
which then satisfies
Kx & (y)(Ky  y = x). y = x).
Hilbert and Bernays continued to use the Greek letter iota
in their individual term, although it has a quite different
grammar from Russell's iota term, since, when Hilbert and
Bernays' term can be introduced, it is provably equivalent to
the corresponding epsilon term (Kneebone 1963, p102). In fact
it was later suggested by many that epsilon terms are not only
complete symbols, but can be seen as playing the same role as
the 'logically proper names' Russell discussed.
It is at the start of book 2 of the Grundlagen that
we find the definition of epsilon terms. There, Hilbert and
Bernays first construct a theory of indefinite descriptions in
a similar manner to their theory of definite descriptions.
They allow, now, an eta term to be introduced as long as just
the first of Russell's conditions is met. That is to say,
given
( x)Fx, x)Fx,
one can introduce the term ' xFx', and say xFx', and say
F xFx. xFx.
But the condition for the introduction of the eta term can
be established logically, for certain predicates, since
( x)(( x)(( y)Fy y)Fy  Fx), Fx),
is a predicate calculus theorem (Copi 1973, p110). It is
the eta term this theorem allows us to introduce which is
otherwise called an epsilon term, and its logical basis
enables entirely formal theories to be constructed, since such
individual terms are invariably defined. Thus we may
invariably introduce ' x(( x(( y)Fy y)Fy  Fx)', and this is commonly written ' Fx)', and this is commonly written ' xFx', about which we can therefore say xFx', about which we can therefore say
( y)Fy y)Fy  F F xFx. xFx.
Since it is that F which exists if anything is F, Hilbert
read the epsilon term in this case 'the first F'. For
instance, in arithmetic, 'the first' may be taken to be the
least number operator. However, while if there are F's then
the first F is clearly some chosen one of them, if there are
no F's then 'the first F' must be a misnomer. And that form of
speech only came to be fully understood in the theories of
reference which appeared much later, when reference and
denotation came to be more clearly separated from description
and attribution. Donnellan (Donnellan 1966) used the example
'the man with martini in his glass', and pointed out that, in
certain uses, this can refer to someone without martini in his
glass. In the terminology Donnellan made popular, 'the first
F', in the second case above works similarly: it cannot be
attributive, and so, while it refers to something, it must
refer arbitrarily, from a semantic point of view.
With reference in this way separated from attribution it
becomes possible to symbolise the anaphoric cross-reference
between, for instance, 'There is one and only one king of
France' and 'He is bald'. For, independently of whether the
former is true, the 'he' in the latter is a pronoun for the
epsilon term in the former -- by a simple extension of the
epsilon definition of the existential quantifier. Thus the
pair of remarks may be symbolised
( x)(Kx & (y)(Ky x)(Kx & (y)(Ky  y = x)) & B y = x)) & B x(Kx & (y)(Ky x(Kx & (y)(Ky  y = x)). y = x)).
Furthermore such cross-reference may occur in connection
with intensional constructions of a kind Russell also
considered, such as
George IV wondered whether the author of Waverley was
Scott.
Thus we can say 'There is an author of Waverley, and George
IV wondered whether he was Scott'. But the epsilon analysis of
these cases puts intensional epsilon calculi at odds with
Russellian views of such constructions, as we shall see later.
The Russellian approach, by not having complete symbols for
individuals, tends to confuse cases in which assertions are
made about individuals and cases in which assertions are made
about identifying properties. As we shall see, epsilon terms
enable us to make the discrimination between, for
instance,
s =  x(y)(Ay x(y)(Ay  y = x), y = x),
(i.e. 'Scott is the author of Waverley'), and
(y)(Ay  y = s), y = s),
(i.e. 'there is one and only one author of Waverley and he
is Scott'), and so it enables us to locate more exactly the
object of George IV's thought.
2. Descriptions and Identity
When one starts to ask about the natural language meaning
of epsilon terms, it is interesting that Leisenring just
mentions the 'formal superiority' of the epsilon calculus
(Leisenring 1969, p63, see also Routley 1969, Hazen 1987).
Leisenring took the epsilon calculus to be a better logic than
the predicate calculus, but merely because of the Second
Epsilon Theorem. Its main virtue, to Leisenring, was that it
could prove all that seemingly needed to be proved, but in a
more elegant way. Epsilon terms were just neater at
calculating which were the valid theorems of the predicate
calculus.
Remembering Hilbert and Bernays' discussion of definite and
indefinite descriptions, clearly there is more to the epsilon
calculus than this. And there are, in fact, two specific
theorems provable within the epsilon calculus, though not the
predicate calculus, which will start to indicate the epsilon
calculus' more general range of application. They concern
individuals, since the epsilon calculus is distinctive in
providing an appropriate, and systematic means of reference to
them.
The need to have complete symbols for individuals became
evident some years after Russell's promotion of incomplete
symbols for them. The first major book to allow for this was
Rosser's Logic for Mathematicians, in 1953, although
there were precursors. For the classical difficulty with
providing complete terms for individuals concerns what to do
with 'non-denoting' terms, and Quine, for instance, following
Frege, often gave them an arbitrary, though specific referent
(Marciszewski 1981, p113). This idea is also present in Kalish
and Montague (Kalish and Montague 1964, pp242-243), who gave
the two rules:
( x)(y)(Fy x)(y)(Fy  y = x) y = x)  F F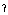 xFx, xFx,
¼( x)(y)(Fy x)(y)(Fy  y = x) y = x)  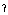 xFx = xFx = 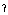 x¼(x = x), x¼(x = x),
where '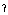 xFx' is what otherwise might be
written ' xFx' is what otherwise might be
written ' x(y)(Fy x(y)(Fy  y = x)'. Kalish and Montague believed,
however, that the second rule 'has no intuitive counterpart,
simply because ordinary language shuns improper definite
descriptions' (Kalish and Montague 1964, p244). And, at that
time, what Donnellan was to publish in Donnellan 1966, about
improper definite descriptions, was certainly not well known.
In fact ordinary speech does not shun improper definite
descriptions, although their referents are not as fixed as the
above second rule requires. Indeed the very fact that the
descriptions are improper means that their referents are not
determined semantically: instead they are just a practical,
pragmatic choice. y = x)'. Kalish and Montague believed,
however, that the second rule 'has no intuitive counterpart,
simply because ordinary language shuns improper definite
descriptions' (Kalish and Montague 1964, p244). And, at that
time, what Donnellan was to publish in Donnellan 1966, about
improper definite descriptions, was certainly not well known.
In fact ordinary speech does not shun improper definite
descriptions, although their referents are not as fixed as the
above second rule requires. Indeed the very fact that the
descriptions are improper means that their referents are not
determined semantically: instead they are just a practical,
pragmatic choice.
Stalnaker and Thomason recognised the need to be more
liberal when they defined their referential terms, which also
had to refer, in the contexts they were concerned with, in
more than one possible world (Thomason and Stalnaker 1968,
p363):
In contrast with the Russellian analysis,
definite descriptions are treated as genuine singular terms;
but in general they will not be substance terms [rigid
designators]. An expression like 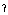 xPx is assigned a referent which
may vary from world to world. If in a given world there is a
unique existing individual which has the property
corresponding to P, this individual is the referent of xPx is assigned a referent which
may vary from world to world. If in a given world there is a
unique existing individual which has the property
corresponding to P, this individual is the referent of 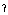 xPx; otherwise, xPx; otherwise, 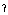 xPx refers to an arbitrarily chosen
individual which does not exist in that world. xPx refers to an arbitrarily chosen
individual which does not exist in that world.
Stalnaker and Thomason appreciated that 'A substance term
is much like what Russell called a logically proper name', but
they said that an individual constant might or might not be a
substance term, depending on whether it was more like
'Socrates' or 'Miss America' (Thomason and Stalnaker 1968,
p362). A more complete investigation of identity and
descriptions, in modal and general intensional contexts, was
provided in Routley, Meyer and Goddard 1974, and Routley 1977,
see also Hughes and Cresswell 1968, Ch 11. And with these
writers we get the explicit rendering of definite descriptions
in epsilon terms, as in Goddard and Routley 1973, p558,
Routley 1980, p277, c.f. Hughes and Cresswell 1968, p203.
Certain specific theorems in the epsilon calculus, as was
said before, support these kinds of identification. One
theorem demonstrates directly the relation between Russell's
attributive, and some of Donnellan's referential ideas.
For
( x)(Fx & (y)(Fy x)(Fx & (y)(Fy  y = x) & Gx) y = x) & Gx)
is logically equivalent to
( x)(Fx & (y)(Fy x)(Fx & (y)(Fy  y = x)) & Ga, y = x)) & Ga,
where a =  x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x)). This arises because the latter is
equivalent to y = x)). This arises because the latter is
equivalent to
Fa & (y)(Fy  y = a) & Ga, y = a) & Ga,
which entails the former. But the former is
Fb & (y)(Fy  y = b) & Gb, y = b) & Gb,
with b =  x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x) & Gx), and so entails y = x) & Gx), and so entails
( x)(Fx & (y)(Fy x)(Fx & (y)(Fy  y = x)), y = x)),
and
Fa & (y)(Fy  y = a). y = a).
But that means that, from the uniqueness clause,
a = b,
and so
Ga,
meaning the former entails the latter, and therefore the
former is equivalent to the latter.
The former, of course, gives Russell's Theory of
Descriptions, in the case of 'The F is G'; it explicitly
asserts the first two clauses, to do with the existence and
uniqueness of an F. A presuppositional theory, such as we saw
in Hilbert and Bernays, would not explicitly assert these two
clauses: on such an account they are a precondition before the
term 'the F' can be introduced. But neither of these theories
accommodate improper definite descriptions. Since Donnellan it
is more common to allow that we can always use 'the F': if the
description is improper then the referent of this term is
simply found in the term's practical use.
One detail of Donnellan's historical account, however, must
be treated with some care, at this point. Donnellan was
himself concerned with definite descriptions which were
improper in the sense that they did not uniquely describe what
the speaker took to be their referent. So the description
might still be 'proper' in the above sense -- if there still
was something to which it uniquely applied, on account of its
semantic content. Thus Donnellan allowed 'the man with martini
in his glass' to identify someone without martini in his glass
irrespective of whether there was some sole man with martini
in his glass. But if one talks about 'the man with martini in
his glass' one can be correctly taken to be talking about who
this describes, if it does in fact correctly describe someone
-- as Devitt and Bertolet pointed out in criticism of
Donnellan (Devitt 1974, Bertolet 1980). It is this aspect of
our language which the epsilon account matches, for an epsilon
account allows definite descriptions to refer without
attribution of their semantic character, but only if nothing
uniquely has that semantic character. Thus it is not the whole
of the first statement above , but only the third part of the
second statement which makes the remark 'The F is G'.
The difficulty with Russell's account becomes more plain if
we read the two equivalent statements using relative and
personal pronouns. They then become
There is one and only one F, which is G,
There is one
and only one F; it is G.
But using just the logic derived from Frege, Russell could
formalise the 'which', but could not separate out the last
clause, 'it is G'. In that clause 'it' is an anaphor for 'the
(one and only) F', and it still has this linguistic meaning if
there is no such thing, since that is just a matter of
grammar. But the uniqueness clause is needed for the two
statements to be equivalent -- without uniqueness there is no
equivalence, as we shall see - so 'which' is not itself
equivalent to 'it'. Russell, however, because he could not
separate out the 'it', had to take the whole of the first
expression as the analysis of 'The F is G' -- he could not
formulate the needed 'logically proper name'.
But how can something be the one and only F 'if there is no
such thing'? That is where another important theorem provable
in the epsilon calculus is illuminating, viz:
(Fa & (y)(Fy  y = a)) y = a))  a = a =  x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x)). y = x)).
The important thing is that there is a difference between
the left hand side and the right hand side, i.e. between
something being alone F, and that thing being the one and only
F. For the left-right implication cannot be reversed. We get
from the left to the right when we see that the left as a
whole entails
( x)(Fx & (y)(Fy x)(Fx & (y)(Fy  y = x)), y = x)),
and so also its epsilon equivalent
F x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x)) & (z)(Fz y = x)) & (z)(Fz  z = z =  x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x))). y = x))).
Given Fa, then from the second clause here we get the right
hand side of our original implication. But if we substitute
' x(Fx & (y)(Fy x(Fx & (y)(Fy  y = x))' for 'a' in that implication then on
the right we have something which is necessarily true. But the
left hand side is then the same as y = x))' for 'a' in that implication then on
the right we have something which is necessarily true. But the
left hand side is then the same as
( x)(Fx & (y)(Fy x)(Fx & (y)(Fy  y = x)), y = x)),
and that is in general contingent. Hence the implication
cannot generally be reversed. Having the property of being
alone F is here contingent, but possessing the identity of the
one and only F is necessary.
The distinction is not made in Russell's logic, since
possession of the relevant property is the only thing which
can be formally expressed there. In Russell's theory of
descriptions, a's possession of the property of being alone a
king of France is expressed as a quasi identity
a = 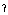 xKx, xKx,
and that has the consequence that such identities are
contingent. Indeed, in counterpart theories of objects in
other possible worlds the idea is pervasive that an entity may
be defined in terms of its contingent properties in a given
world. Hughes and Cresswell, however, differentiated between
contingent identities and necessary identities in the
following way (Hughes and Cresswell 1968, p191):
Now it is contingent that the man who is in fact
the man who lives next door is the man who lives next door,
for he might have lived somewhere else; that is living next
door is a property which belongs contingently, not
necessarily, to the man to whom it does belong. And
similarly, it is contingent that the man who is in fact the
mayor is the mayor; for someone else might have been elected
instead. But if we understand [The man who lives next door
is the mayor] to mean that the object which (as a matter of
contingent fact) possesses the property of being the man who
lives next door is identical with the object which (as a
matter of contingent fact) possesses the property of being
the mayor, then we are understanding it to assert that a
certain object (variously described) is identical with
itself, and this we need have no qualms about regarding as a
necessary truth. This would give us a way of construing
identity statements which makes [(x = y)  L(x = y)] perfectly acceptable: for
whenever x = y is true we can take it as expressing the
necessary truth that a certain object is identical with
itself. L(x = y)] perfectly acceptable: for
whenever x = y is true we can take it as expressing the
necessary truth that a certain object is identical with
itself.
There are more consequences of this matter, however, than
Hughes and Cresswell drew out. For now that we have proper
referring terms for individuals to go into such expressions as
'x = y', we first see better where the contingency of the
properties of such individuals comes from -- simply the
linguistic facility of using improper definite descriptions.
But we also see, because identities between such terms are
necessary, that proper referring terms must be rigid, i.e.
have the same reference in all possible worlds.
This is not how Stalnaker and Thomason saw the matter.
Stalnaker and Thomason, it will be remembered, said that there
were two kinds of individual constants: ones like 'Socrates'
which can take the place of individual variables, and others
like 'Miss America' which cannot. The latter, as a result,
they took to be non-rigid. But it is strictly 'Miss America in
year t' which is meant in the second case, and that is not a
constant expression, even though such functions can take the
place of individual variables. It was Routley, Meyer and
Goddard who most seriously considered the resultant
possibility that all properly individual terms are rigid. At
least, they worked out many of the implications of this
position, even though Routley was not entirely content with
it.
Routley described several rigid intensional semantics
(Routley 1977, pp185-186). One of these, for instance, just
took the first epsilon axiom to hold in any interpretation,
and made the value of an epsilon term itself. On such a basis
Routley, Meyer and Goddard derived what may be called
'Routley's Formula', i.e.
L( x)Fx x)Fx  ( ( x)LFx. x)LFx.
In fact, on their understanding, this formula holds for any
operator and any predicate, but they had in mind principally
the case of necessity illustrated here, with 'Fx' taken as 'x
numbers the planets', making ' xFx' 'the number of the planets'. The formula
is derived quite simply, in the following way: from xFx' 'the number of the planets'. The formula
is derived quite simply, in the following way: from
L( x)Fx, x)Fx,
we can get
LF xFx, xFx,
by the epsilon definition of the existential quantifier,
and so
( x)LFx, x)LFx,
by existential generalisation over the rigid term (Routley,
Meyer and Goddard 1974, p308, see also Hughes and Cresswell
1968, pp197, 204). Routley, however, was still inclined to
think that a rigid semantics was philosophically objectionable
(Routley 1977, p186):
Rigid semantics tend to clutter up the semantics
for enriched systems with ad hoc modelling conditions. More
important, rigid semantics, whether substitutional or
objectual, are philosophically objectionable. For one thing,
they make Vulcan and Hephaestus everywhere indistinguishable
though there are intensional claims that hold of one but not
of the other. The standard escape from this sort of problem,
that of taking proper names like 'Vulcan' as disguised
descriptions we have already found wanting... Flexible
semantics, which satisfactorily avoid these objections,
impose a more objectual interpretation, since, even if [the
domain] is construed as the domain of terms, [the value of a
term in a world] has to be permitted, in some cases at
least, to vary from world to world.
As a result, while Routley, Meyer and Goddard were still
prepared to defend the formula, and say, for instance, that
there was a number which necessarily numbers the planets,
namely the number of the planets (np), they thought that this
was only in fact the same as 9, so that one still could not
argue correctly that as L(np numbers the planets), so L(9
numbers the planets). 'For extensional identity does not
warrant intersubstitutivity in intensional frames' (Routley,
Meyer and Goddard 1974, p309). They held, in other words that
the number of the planets was only contingently 9.
This means that they denied '(x = y)  L(x = y)', but, as we shall see in more
detail later, there are ways to hold onto this principle, i.e.
maintain the invariable necessity of identity. L(x = y)', but, as we shall see in more
detail later, there are ways to hold onto this principle, i.e.
maintain the invariable necessity of identity.
3. Rigid Epsilon Terms
There is some further work which has helped us to
understand how reference in modal and general intensional
contexts must be rigid. But it involves some different ideas
in semantics, and starts, even, outside our main area of
interest, namely predicate logic, in the semantics of
propositional logic.
When one thinks of 'semantics' one maybe thinks of the
valuation of formulas. Since the 1920s a meta-study of this
kind was certainly added to the previous logical interest in
proof theory. Traditional proof theory is commonly associated
with axiomatic procedures, but, from a modern perspective, its
distinction is that it is to do with 'object languages'.
Tarski's theory of truth relies crucially on the distinction
between object languages and meta-languages, and so semantics
generally seems to be necessarily a meta-discipline. In fact
Tarski believed that such an elevation of our interest was
forced upon us by the threat of semantic paradoxes like The
Liar. If there was, by contrast, 'semantic closure', i.e. if
truth and other semantic notions were definable at the object
level, then there would be contradictions galore (c.f. Priest
1984). In this way truth may seem to be necessarily a
predicate of (object-level) sentences.
But there is another way of looking at the matter which is
explicitly non-Tarskian, and which others have followed (see
Prior 1971, Ch 7, Sayward 1987). This involves seeing 'it is
true that' as not a predicate, but an object-level operator,
with the truth tabulations in Truth Tables, for instance,
being just another form of proof procedure. Operators indeed
include 'it is provable that', and this is distinct from
G÷del's provability predicate, as G÷del himself pointed out
(G÷del 1969). Operators are intensional expressions, as in the
often discussed 'it is necessary that' and 'it is believed
that', and trying to see such forms of indirect discourse as
metalinguistic predicates was very common in the middle of the
last century. It was pervasive, for instance, in Quine's many
discussions of modality and intensionality. Wouldn't someone
be believing that the Morning Star is in the sky, but the
Evening Star is not, if, respectively, they assented to the
sentence 'the Morning Star is in the sky', and dissented from
'the Evening Star is in the sky'? Anyone saying 'yes' is still
following the Quinean tradition, but after Montague's and
Thomason's work on operators (e.g. Montague 1963, Thomason
1977, 1980) many logicians are more persuaded that indirect
discourse is not quotational. It is open to doubt, that is to
say, whether we should see the mind in terms of the direct
words which the subject would use.
The alternative involves seeing the words 'the Morning Star
is in the sky' in such an indirect speech locution as 'Quine
believes that the Morning Star is in the sky' as words merely
used by the reporter, which need not directly reflect what the
subject actually says. That is indeed central to reported
speech -- putting something into the reporter's own words
rather than just parroting them from another source. Thus a
reporter may say
Celia believed that the man in the room was a woman,
but clearly that does not mean that Celia would use 'the
man in the room' for who she was thinking about. So
referential terms in the subordinate proposition are only
certainly in the mouth of the reporter, and as a result only
certainly refer to what the reporter means by them. It is a
short step from this thought to seeing
There was a man in the room, but Celia believed that he was
a woman,
as involving a transparent intensional locution, with the
same object, as one might say, 'inside' the belief as
'outside' in the room. So it is here where rigid constant
epsilon terms are needed, to symbolise the cross-sentential
anaphor 'he', as in:
( x)(Mx & Rx) & BcW x)(Mx & Rx) & BcW x(Mx & Rx). x(Mx & Rx).
To understand the matter fully, however, we must make the
shift from meta- to object language we saw at the
propositional level above with truth. Routley, Meyer and
Goddard realised that a rigid semantics required treating such
expressions as 'BcWx' as simple predicates, and we must now
see what this implies. They derived, as we saw before,
'Routley's Formula'
L( x)Fx x)Fx  ( ( x)LFx, x)LFx,
but we can now start to spell out how this is to be
understood, if we hold to the necessity of identities, i.e. if
we use '=' so that
x = y  L(x = y). L(x = y).
Again a clear illustration of the validity of Routley's
Formula is provided by the number of the planets, but now we
may respect the fact that some things may lack a number, and
also the fact that referential, and attributive senses of
terms may be distinguished. Thus if we write '(nx)Px' for
'there are n P's', then  n(ny)Py will be the number of P's, and it is
what numbers them (i.e. ([ n(ny)Py will be the number of P's, and it is
what numbers them (i.e. ([ n(ny)Py]x)Px) if they have a number (i.e. if
( n(ny)Py]x)Px) if they have a number (i.e. if
( n)(nx)Px) -- by the epsilon definition of the
existential quantifier. Then, with 'Fx' as the proper
(necessary) identity 'x = n)(nx)Px) -- by the epsilon definition of the
existential quantifier. Then, with 'Fx' as the proper
(necessary) identity 'x =  n(ny)Py' Routley's Formula holds because the
number in question exists eternally, making both sides of the
formula true. But if 'Fn' is simply the attributive '(ny)Py'
then this is not necessary, since it is contingent even, in
the first place, that there is a number of P's, instead of
just some P, making both sides of the formula false. n(ny)Py' Routley's Formula holds because the
number in question exists eternally, making both sides of the
formula true. But if 'Fn' is simply the attributive '(ny)Py'
then this is not necessary, since it is contingent even, in
the first place, that there is a number of P's, instead of
just some P, making both sides of the formula false.
Hughes and Cresswell argue against the principle saying
(Hughes and Cresswell 1968, p144):
...let [Fx] be 'x is the number of the planets'.
Then the antecedent is true, for there must be some number
which is the number of the planets (even if there were no
planets at all there would still be such a number, viz. 0):
but the consequent is false, for since it is a contingent
matter how many planets there are, there is no number which
must be the number of the planets.
But this forgets continuous quantities, where there are no
discrete items before the nomination of a unit. The number
associated with some planetary material, for instance, numbers
only arbitrary units of that material, and not the material
itself. So the antecedent of Routley's Formula is not
necessarily true.
Quine also used the number of the planets in his central
argument against quantification into modal contexts. He said
(Quine 1960, pp195-197):
If for the sake of argument we accept the term 'analytic'
as predicable of sentences (hence as attachable
predicatively to quotations or other singular terms
designating sentences), then 'necessarily' amounts to 'is
analytic' plus an antecedent pair of quotation marks. For
example, the sentence:
(1) Necessarily 9 > 4
is explained thus:
(2) '9 > 4' is analytic...
So suppose (1) explained as in (2). Why, one may ask,
should we preserve the operatorial form as of (1), and
therewith modal logic, instead of just leaving matters as in
(2)? An apparent advantage is the possibility of quantifying
into modal positions; for we know we cannot quantify into
quotation, and (2) uses quotation...
But is it more legitimate to quantify into modal
positions than into quotation? For consider (1) even without
regard to (2); surely, on any plausible interpretation, (1)
is true and this is false:
(3) Necessarily the number of major planets > 4.
Since 9 = the number of major planets, we can conclude
that the position of '9' in (1) is not purely referential
and hence that the necessity operator is
opaque.
But here Quine does not separate out the referential 'the
number of the major planets is greater than 4', i.e. ' n(ny)Py > 4', from the attributive 'There
are more than 4 major planets', i.e. '( n(ny)Py > 4', from the attributive 'There
are more than 4 major planets', i.e. '( n)((ny)Py & n > 4)'. If 9 = n)((ny)Py & n > 4)'. If 9 =  n(ny)Py, then it follows that n(ny)Py, then it follows that  n(ny)Py > 4, but it does not follow that
( n(ny)Py > 4, but it does not follow that
( n)((ny)Py & n > 4). Substitution of
identicals in (1), therefore, does yield (3), even though it
is not necessary that there are more than 4 major planets. n)((ny)Py & n > 4). Substitution of
identicals in (1), therefore, does yield (3), even though it
is not necessary that there are more than 4 major planets.
We can now go into some details of how one gets the 'x' in
such a form as 'LFx' to be open for quantification. For, what
one finds in traditional modal semantics (see Hughes and
Cresswell 1968, passim) are formulas in the meta-linguistic
style, like
V(Fx, i) = 1,
which say that the valuation put on 'Fx' is 1, in world i.
There should be quotation marks around the 'Fx' in such a
formula, to make it meta-linguistic, but by convention they
are generally omitted. To effect the change to the
non-meta-linguistic point of view, we must simply read this
formula as it literally is, so that the 'Fx' is in indirect
speech rather than direct speech, and the whole becomes the
operator form 'it would be true in world i that Fx'. In this
way, the term 'x' gets into the language of the reporter, and
the meta/object distinction is not relevant. Any variable
inside the subordinate proposition can now be quantified over,
just like a variable outside it, which means there is
'quantifying in', and indeed all the normal predicate logic
operations apply, since all individual terms are rigid.
A example illustrating this rigidity involves the actual
top card in a pack, and the cards which might have been top
card in other circumstances (see Slater 1988a). If the actual
top card is the Ace of Spades, and it is supposed that the top
card is the Queen of Hearts, then clearly what would have to
be true for those circumstances to obtain would be for the Ace
of Spades to be the Queen of Hearts. The Ace of Spades is not
in fact the Queen of Hearts, but that does not mean they
cannot be identical in other worlds (c.f. Hughes and
Cresswell, 1968, p190). Certainly if there were several cards
people variously thought were on top, those cards in the
various supposed circumstances would not provide a constant c
such that Fc is true in all worlds. But that is because those
cards are functions of the imagined worlds -- the card a
believes is top ( xBaFx) need not be the card b believes is top
( xBaFx) need not be the card b believes is top
( xBbFx), etc. It still remains that there is a
constant, c, such that Fc is true in all worlds. Moreover,
that c is not an 'intensional object', for the given Ace of
Spades is a plain and solid extensional object, the actual top
card ( xBbFx), etc. It still remains that there is a
constant, c, such that Fc is true in all worlds. Moreover,
that c is not an 'intensional object', for the given Ace of
Spades is a plain and solid extensional object, the actual top
card ( xFx). xFx).
Routley, Meyer and Goddard did not accept the latter point,
wanting a rigid semantics in terms of 'intensional objects'
(Goddard and Routley, 1973, p561, Routley, Meyer and Goddard,
1974, p309, see also Hughes and Cresswell 1968, p197).
Stalnaker and Thomason accepted that certain referential terms
could be functional, when discriminating 'Socrates' from 'Miss
America' -- although the functionality of 'Miss America in
year t' is significantly different from that of 'the top card
in y's belief'. For if this year's Miss America is last year's
Miss America, still it is only one thing which is identical
with itself, unlike with the two cards. Also, there is nothing
which can force this year's Miss America to be last year's
different Miss America, in the way that the counterfactuality
of the situation with the playing cards forces two
non-identical things in the actual world to be the same thing
in the other possible world. Other possible worlds are thus
significantly different from other times, and so, arguably,
other possible worlds should not be seen from the Realist
perspective appropriate for other times -- or other
spaces.
4. The Epsilon Calculus'
Problematic
It might be said that Realism has delayed a proper logical
understanding of many of these things. If you look
'realistically' at picturesque remarks like that made before,
namely 'the same object is 'inside' the belief as 'outside' in
the room', then it is easy for inappropriate views about the
mind to start to interfere, and make it seem that the same
object cannot be in these two places at once. But if the mind
were something like another space or time, then
counterfactuality could get no proper purchase -- no one could
be 'wrong', since they would only be talking about elements in
their 'world', not any objective, common world. But really,
all that is going on when one says, for instance,
There was a man in the room, but Celia believed he was a
woman,
is that the same term -- or one term and a pronominal
surrogate for it -- appears at two linguistic places in some
discourse, with the same reference. Hence there is no
grammatical difference between the cross reference in such an
intensional case and the cross reference in a non-intensional
case, such as
There was a man in the room. He was hungry.
i.e.
( x)Mx & H x)Mx & H xMx. xMx.
What has been difficult has merely been getting a
symbolisation of the cross-reference in this more elementary
kind of case. But it just involves extending the epsilon
definition of existential statements, using a reiteration of
the substituted epsilon term, as we can see.
It is now widely recognised how the epsilon calculus allows
us to do this (Purdy 1994, Egli and von Heusinger 1995, Meyer
Viol 1995, Ch 6), the theoretical starting point being the
theorem about the Russellian theory of definite descriptions
proved before, which breaks up what otherwise would be a
single sentence into a sequential piece of discourse, enabling
the existence and uniqueness clauses to be put in one sentence
while the characterising remark is in another. The
relationship starts to matter when, in fact, there is no
obvious way to formulate a combination of anaphoric remarks in
the predicate calculus, as in, for instance,
There is a king of France. He is bald,
where there is no uniqueness clause. This difficulty became
a major problem when logicians started to consider anaphoric
reference in the 1960s.
Geach, for instance, in Geach 1962, even believed there
could not be a syllogism of the following kind (Geach 1962,
p126):
A man has just drunk a pint of sulphuric acid.
Nobody
who drinks a pint of sulphuric acid lives through the
day.
So, he won't live through the day.
He said, one could only draw the conclusion:
Some man who has just drunk a pint of sulphuric acid won't
live through the day.
Certainly one can only derive
( x)(Mx & Dx & ¼Lx) x)(Mx & Dx & ¼Lx)
from
( x)(Mx & Dx), x)(Mx & Dx),
and
(x)(Dx  ¼Lx), ¼Lx),
within predicate logic. But one can still derive
¼L x(Mx & Dx), x(Mx & Dx),
within the epsilon calculus.
Geach likewise was foxed later when he produced his famous
case (numbered 3 in Geach 1967):
Hob thinks a witch has blighted Bob's mare, and Nob
wonders whether she (the same witch) killed Cob's
sow,
which is, in epsilon terms
Th( x)(Wx & Bxb) & OnK x)(Wx & Bxb) & OnK x(Wx & Bxb)c. x(Wx & Bxb)c.
For Geach saw that this could not be (4)
( x)(Wx & ThBxb & OnKxc), x)(Wx & ThBxb & OnKxc),
or (5)
( x)(Th(Wx & Bxb)& OnKxc). x)(Th(Wx & Bxb)& OnKxc).
But also a reading of the second clause as (c.f. 18)
Nob wonders whether the witch who blighted Bob's mare
killed Cob's sow,
in which 'the witch who blighted Bob's mare killed Cob's
sow' is analysed in the Russellian manner, i.e. as (20)
just one witch blighted Bob's mare and she killed Cob's
sow,
Geach realised does not catch the specific cross-reference
-- amongst other things because of the uniqueness condition
which is then introduced.
This difficulty with the uniqueness clause in Russellian
analyses has been widely commented on, although a recent
theorist, Neale, has said that Russell's theory only needs to
be modestly modified: Neale's main idea is that, in general,
definite descriptions should just be localised to the context.
His resolution of Geach's troubling cases thus involves
suggesting that 'she', in the above, might simply be 'the
witch we have been hearing about' (Neale 1990, p221). Neale
might here have said 'that witch who blighted Bob's mare',
showing that an Hilbertian account of demonstrative
descriptions would have a parallel effect.
A good deal of the ground breaking work on these matters,
however, was done by someone again much influenced by Russell:
Evans. But Evans significantly broke with Russell over
uniqueness (Evans 1977, pp516-517):
One does not want to be committed, by this way
of telling the story, to the existence of a day on which
just one man and boy walked along a road. It was with this
possibility in mind that I stated the requirement for the
appropriate use of an E-type pronoun in terms of having
answered, or being prepared to answer upon demand, the
question 'He? Who?' or 'It? Which?' In order to effect this
liberalisation we should allow the reference of the E-type
pronoun to be fixed not only by predicative material
explicitly in the antecedent clause, but also by material
which the speaker supplies upon demand. This ruling has the
effect of making the truth conditions of such remarks
somewhat indeterminate; a determinate proposition will have
been put forward only when the demand has been made and the
material supplied.
It was Evans who gave us the title 'E-type pronoun' for the
'he' in such expressions as
A Cambridge philosopher smoked a pipe, and he drank a lot
of whisky,
i.e., in epsilon terms,
( x)(Cx & Px) & D x)(Cx & Px) & D x(Cx & Px). x(Cx & Px).
He also insisted (Evans 1977, p516) that what was unique
about such pronouns was that this conjunction of statements
was not equivalent to
A Cambridge philosopher, who smoked a pipe, drank a lot of
whisky,
i.e.
( x)(Cx & Px & Dx). x)(Cx & Px & Dx).
Clearly the epsilon account is entirely in line with this,
since it illustrates the point made before about cases without
a uniqueness clause. Only the second expression, which
contains a relative pronoun, is formalisable in the predicate
calculus. To formalise the first expression, which contains a
personal pronoun, one at least needs something with the
expressive capabilities of the epsilon calculus.
5. The Formal Semantics of Epsilon
Terms
The semantics of epsilon terms is nowadays more general,
but the first interpretations of epsilon terms were restricted
to arithmetical cases, and specifically took epsilon to be the
least number operator. Hilbert and Bernays developed
Arithmetic using the epsilon calculus, using the further
epsilon axiom schema (Hilbert and Bernays 1970, Book 2, p85f,
c.f. Leisenring 1969, p92) :
( xAx = st) xAx = st)  ¼At, ¼At,
where 's' is intended to be the successor function, and 't'
is any numeral. This constrains the interpretation of the
epsilon symbol, but the least number interpretation is not
strictly forced, since the axiom only ensures that no number
having the property A immediately precedes  xAx. xAx.
The new axiom, however, is sufficient to prove mathematical
induction, in the form:
(A0 & (x)(Ax  Asx)) Asx))  (x)Ax. (x)Ax.
For assume the reverse, namely
A0 & (x)(Ax  Asx) & ¼(x)Ax, Asx) & ¼(x)Ax,
and consider what happens when the term ' x¼Ax' is substituted in x¼Ax' is substituted in
t = 0 v t
= sn,
which is derivable from the other axioms of number theory
which Hilbert and Bernays are using. If we had
 x¼Ax = 0, x¼Ax = 0,
then, since it is given that A0, then we would have A x¼Ax. But since, by the definition of the
universal quantifier, x¼Ax. But since, by the definition of the
universal quantifier,
A x¼Ax x¼Ax  (x)Ax, (x)Ax,
we know, because ¼(x)Ax is also given, that ¼A x¼Ax, which means we cannot have x¼Ax, which means we cannot have  x¼Ax = 0. Hence we must have the other
alternative, i.e. x¼Ax = 0. Hence we must have the other
alternative, i.e.
 x¼Ax = sn, x¼Ax = sn,
for some n. But from the new axiom
( x¼Ax = sn) x¼Ax = sn)  An, An,
hence we must have An, although we must also have
An  Asn, Asn,
because (x)(Ax  Asx). All together that requires A Asx). All together that requires A x¼Ax again, which is impossible. Hence the
further epsilon axiom is sufficient to establish the given
principle of induction. x¼Ax again, which is impossible. Hence the
further epsilon axiom is sufficient to establish the given
principle of induction.
The more general link between epsilon terms and choice
functions was first set out by Asser, although Asser's
semantics for an elementary epsilon calculus without the
second epsilon axiom makes epsilon terms denote rather complex
choice functions. Wilfrid Meyer Viol, calling an epsilon
calculus without the second axiom an 'intensional' epsilon
calculus, makes the epsilon terms in such a calculus instead
name Skolem functions. Skolem functions are also called
Herbrand functions, although they arise in a different way,
namely in Skolem's Theorem. Skolem's Theorem states that, if a
formula in prenex normal form is provable in the predicate
calculus, then a certain corresponding formula, with the
existential quantifiers removed, is provable in a predicate
calculus enriched with function symbols. The functions
symbolised are called Skolem functions, although, in another
context, they would be Herbrand functions.
Skolem's Theorem is a meta-logical theorem, about the
relation between two logical calculi, but a non-metalogical
version is in fact provable in the epsilon calculus from which
Skolem's actual theorem follows, since, for example, we can
get, by the epsilon definition, now of the existential
quantifier
(x)( y)Fxy y)Fxy  (x)Fx (x)Fx yFxy. yFxy.
As a result, if the left hand side of such an equivalence
is provable in an epsilon calculus the right hand side is
provable there. But the left hand side is provable in an
epsilon calculus if it is provable in the predicate calculus,
by the Second Epsilon Theorem; and if the right hand side is
provable in an epsilon calculus it is provable in a predicate
calculus enriched with certain function symbols -- epsilon
terms, like ' yFxy'. So, by generalisation, we get Skolem's
original result. yFxy'. So, by generalisation, we get Skolem's
original result.
When we add to an intensional epsilon calculus the second
epsilon axiom
(x)(Fx  Gx) Gx)   xFx = xFx =  xGx, xGx,
the interpretation of epsilon terms is commonly
extensional, i.e. in terms of sets, since two predicates 'F'
and 'G' satisfying the antecedent of this second axiom will
determine the same set -- if they determine sets at all, that
is. For that requires the predicates to be collectivisantes,
in Bourbaki's terms, as with explicit set membership
statements, like 'x 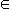 y'. In such a case the epsilon term ' y'. In such a case the epsilon term ' x(x x(x 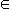 y)' designates a choice function, i.e. a
function which selects one from a given set (c.f. Leisenring
1969, p19, Meyer Viol 1995, p42). In the case where there are
no members of the set the selection is arbitrary, although for
all empty sets it is invariably the same. Thus the second
axiom validates, for example, Kalish and Montague's rule for
this case, which they put in the form y)' designates a choice function, i.e. a
function which selects one from a given set (c.f. Leisenring
1969, p19, Meyer Viol 1995, p42). In the case where there are
no members of the set the selection is arbitrary, although for
all empty sets it is invariably the same. Thus the second
axiom validates, for example, Kalish and Montague's rule for
this case, which they put in the form
 xFx = xFx =  x¼(x = x). x¼(x = x).
Kalish and Montague in fact prove a version of the second
epsilon axiom in their system (Kalish and Montague 1964, see
T407, p256). The second axiom also holds in Hermes' system
(Hermes 1965), although there one in addition finds a third
epsilon axiom,
 x¼(x = x) = x¼(x = x) =  x(x = x), x(x = x),
for which there would seem to be no real justification.
But the second epsilon axiom itself is curious. One
questionable thing about it is that both Leisenring and Meyer
Viol do not state that the predicates in question must
determine sets before their choice function semantics can
apply. That the predicates are collectivisantes is merely
presumed in their theories, since ' xBx' is invariably modelled by means of a
choice from the presumed set of things which in the model are
B. Certainly there is a special clause dealing with the empty
set; but there is no consideration of the case where some
things are B although those things are not discrete, as with
the things which are red, for instance. If the predicate in
question is not a count noun then there is no set of things
involved, since with mass terms, and continuous quantities
there are no given elements to be counted (c.f. Bunt 1985,
pp262-263 in particular). Of course numbers can still be
associated with them, but only given an arbitrary unit. With
the cows in a field, for instance, we can associate a
determinate number, but with the beef there we cannot, unless
we consider, say, the number of pounds of it. xBx' is invariably modelled by means of a
choice from the presumed set of things which in the model are
B. Certainly there is a special clause dealing with the empty
set; but there is no consideration of the case where some
things are B although those things are not discrete, as with
the things which are red, for instance. If the predicate in
question is not a count noun then there is no set of things
involved, since with mass terms, and continuous quantities
there are no given elements to be counted (c.f. Bunt 1985,
pp262-263 in particular). Of course numbers can still be
associated with them, but only given an arbitrary unit. With
the cows in a field, for instance, we can associate a
determinate number, but with the beef there we cannot, unless
we consider, say, the number of pounds of it.
The point, as we saw before, has a formalisation in epsilon
terms. Thus if we write '(nx)Fx', for 'there are n F's', then
 n(ny)Fy will be the number of F's, and it is
what numbers them if they have a number. But in the reverse
case the previously mentioned arbitrariness of the epsilon
term comes in. For if ¼( n(ny)Fy will be the number of F's, and it is
what numbers them if they have a number. But in the reverse
case the previously mentioned arbitrariness of the epsilon
term comes in. For if ¼( n)(nx)Fx, then ¼([ n)(nx)Fx, then ¼([ n(ny)Fy]x)Fx, and so, although an arbitrary
number exists, it does not number the F's. In that case, in
other words, we do not have a number of F's, merely some
F. n(ny)Fy]x)Fx, and so, although an arbitrary
number exists, it does not number the F's. In that case, in
other words, we do not have a number of F's, merely some
F.
In fact, even when there is a set of things, the second
epsilon axiom, as stated above, does not apply in general,
since there are intensional differences between properties to
consider, as in, for instance 'There is a red-haired man, and
a Caucasian in the room, and they are different'. Here, if
there were only red-haired Caucasians in the room, then with
the above second axiom, we could not find epsilon
substitutions to differentiate the two individuals involved.
This may remind us that it is necessary co-extensionality, and
not just contingent co-extensionality which is the normal
criterion for the identity of properties (c.f. Hughes and
Cresswell 1968, pp209-210). So it leads us to see the
appropriateness of a modalised second axiom, which uses just
an intensional version of the antecedent of the previous
second epsilon axiom, in which 'L' means 'it is necessary
that', viz:
L(x)(Fx  Gx) Gx)   xFx = xFx =  xGx. xGx.
For with this axiom only the co-extensionalities which are
necessary will produce identities between the associated
epsilon terms. We can only get, for instance,
 xPx = xPx =  x(Px v Px), x(Px v Px),
and
 xFx = xFx =  yFy, yFy,
and all other identities derivable in a similar way.
However, the original second epsilon axiom is then
provable, in the special case where the predicates express set
membership. For if necessarily
(x)(x 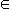 y y  x x 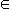 z) z)  y = z, y = z,
while necessarily
y = z  L(y = z), L(y = z),
(see Hughes and Cresswell, 1968, p190) then
L(x)(x 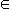 y y  x x 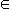 z) z)  (x)(x (x)(x 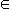 y y  x x 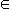 z), z),
and so, from the modalised second axiom we can get
(x)(x 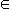 y y  x x 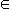 z) z)   x(x x(x 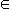 y) = y) =  x(x x(x 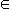 z). z).
Note, however, that if one only has contingently
(x)(Fx  x x 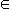 z), z),
then one cannot get, on this basis,
 xFx = xFx =  x(x x(x 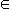 z). z).
But this is something which is desirable, as well. For we
have seen that it is contingent that the number of the planets
does number the planets -- because it is not necessary that
([ n(ny)Py]x)Px. This makes '(9x)Px' contingent,
even though the identity '9 = n(ny)Py]x)Px. This makes '(9x)Px' contingent,
even though the identity '9 =  n(nx)Px' remains necessary. But also it is
contingent that there is the set of planets, p, which there
is, since while, say, n(nx)Px' remains necessary. But also it is
contingent that there is the set of planets, p, which there
is, since while, say,
(x)(x 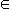 p p  Px), Px),
where
 n(nx)(x n(nx)(x 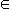 p) = p) =  n(nx)Px = 9, n(nx)Px = 9,
it is still possible that, in some other possible
world,
(x)(x 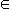 p' p'  Px), Px),
with p' the set of planets there, and
¼( n(nx)(x n(nx)(x 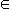 p') = 9). p') = 9).
We could not have this further contingency, however, if the
original second epsilon axiom held universally.
It is on this fuller basis that we can continue to hold 'x
= y  L(x = y)', i.e. the invariable necessity of
identity -- one merely distinguishes '(9x)Px' from '9 = L(x = y)', i.e. the invariable necessity of
identity -- one merely distinguishes '(9x)Px' from '9 =  x(nx)Px', and from '9 = x(nx)Px', and from '9 =  x(nx)(x x(nx)(x 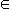 p)', as above. p)', as above.
Adding the original second epsilon axiom to an intensional
epsilon calculus is therefore acceptable only if all the
predicates are about set membership. This is not an uncommon
assumption, indeed it is pervasive in the usually given
semantics for predicate logic, for instance. But if, by
contrast, we want to allow for the fact that not all
predicates are collectivisantes then we should take just the
first epsilon axiom with merely a modalised version of the
second epsilon axiom. The interpretation of epsilon terms is
then always in terms of Skolem functions, although if we are
dealing with the membership of sets, those Skolem functions
naturally are choice functions.
6. Some Metatheory
To finish we shall briefly look, as promised, at some
meta-theory.
The epsilon calculi that were first described were not very
convenient to use, and Hilbert and Bernays' proofs of the
First and Second Epsilon Theorems were very complex. This was
because the presentation was axiomatic, however, and with the
development of other means of presenting the same logics we
get more readily available meta-logical results. I will
indicate some of the early difficulties before showing how
these theorems can be proved, nowadays, much more simply.
The problem with proving the Second Epsilon Theorem, on an
axiomatic basis, is that complex, and non-constant epsilon
terms may enter a proof in the epsilon calculus by means of
substitutions into the axioms. What has to be proved is that
an epsilon calculus proof of an epsilon-free theorem (i.e. one
which can be expressed just in predicate calculus language)
can be replaced by a predicate calculus proof. So some
analysis of complex epsilon terms is required, to show that
they can be eliminated in the relevant cases, leaving only
constant epsilon terms, which are sufficiently similar to the
individual symbols in standard predicate logic. Hilbert and
Bernays (Hilbert and Bernays 1970, Book 2, p23f) say that one
epsilon term ' xFx' is subordinate to another ' xFx' is subordinate to another ' yGy' if and only if 'G' contains ' yGy' if and only if 'G' contains ' xFx', and a free occurrence of the variable
'y' lies within ' xFx', and a free occurrence of the variable
'y' lies within ' xFx'. For instance ' xFx'. For instance ' xRxy' is a complex, and non-constant epsilon
term, which is subordinate to ' xRxy' is a complex, and non-constant epsilon
term, which is subordinate to ' ySy ySy xRyx'. Hilbert and Bernays then define the
rank of an epsilon term to be 1 if there are no epsilon terms
subordinate to it, and otherwise to be one greater than the
maximal rank of the epsilon terms which are subordinate to it.
Using the same general ideas, Leisenring proves two theorems
(Leisenring 1969, p72f). First he proves a rank reduction
theorem, which shows that epsilon proofs of epsilon-free
formulas in which the second epsilon axiom is not used, but in
which every term is of rank less than or equal to r, may be
replaced by epsilon proofs in which every term is of rank less
than or equal to r - 1. Then he proves the eliminability of
the second epsilon axiom in proofs of epsilon-free formulas.
Together, these two theorems show that if there is an epsilon
proof of an epsilon-free formula, then there is such a proof
not using the second epsilon axiom, and in which all epsilon
terms have rank just 1. Even though such epsilon terms might
still contain free variables, if one replaces those that do
with a fixed symbol 'a' (starting with those of maximal
length) that reduces the proof to one in what is called the
'epsilon star' system, in which there are only constant
epsilon terms (Leisenring 1969, p66f). Leisenring shows that
proofs in the epsilon star system can be turned into proofs in
the predicate calculus, by replacing the epsilon terms by
individual symbols. xRyx'. Hilbert and Bernays then define the
rank of an epsilon term to be 1 if there are no epsilon terms
subordinate to it, and otherwise to be one greater than the
maximal rank of the epsilon terms which are subordinate to it.
Using the same general ideas, Leisenring proves two theorems
(Leisenring 1969, p72f). First he proves a rank reduction
theorem, which shows that epsilon proofs of epsilon-free
formulas in which the second epsilon axiom is not used, but in
which every term is of rank less than or equal to r, may be
replaced by epsilon proofs in which every term is of rank less
than or equal to r - 1. Then he proves the eliminability of
the second epsilon axiom in proofs of epsilon-free formulas.
Together, these two theorems show that if there is an epsilon
proof of an epsilon-free formula, then there is such a proof
not using the second epsilon axiom, and in which all epsilon
terms have rank just 1. Even though such epsilon terms might
still contain free variables, if one replaces those that do
with a fixed symbol 'a' (starting with those of maximal
length) that reduces the proof to one in what is called the
'epsilon star' system, in which there are only constant
epsilon terms (Leisenring 1969, p66f). Leisenring shows that
proofs in the epsilon star system can be turned into proofs in
the predicate calculus, by replacing the epsilon terms by
individual symbols.
But, as was said before, there is now available a much
shorter proof of the Second Epsilon Theorem. In fact there are
several, but I shall just indicate one, which arises simply by
modifying the predicate calculus truth trees, as found in, for
instance, Jeffrey (see Jeffrey 1967). Jeffrey uses the
standard propositional truth tree rules, together with the
rules of quantifier interchange, which remain unaffected, and
which are not material to the present purpose. He also has,
however, a rule of existential quantifier elimination,
( x)Fx x)Fx  Fa, Fa,
in which 'a' must be new, and a rule of universal
quantifier elimination
(x)Fx  Fb, Fb,
in which 'b' must be old -- unless no other individual
terms are available. By reducing closed formulas of the form
'P & ¼C' to absurdity Jeffrey can then prove 'P  C', and validate 'P C', and validate 'P  C' in his calculus. But
clearly, upon adding epsilon terms to the language, the first
of these rules must be changed to C' in his calculus. But
clearly, upon adding epsilon terms to the language, the first
of these rules must be changed to
( x)Fx x)Fx  F F xFx, xFx,
while also the second rule can be replaced by the pair
(x)Fx  F F x¼Fx, x¼Fx,
F x¼Fx x¼Fx  Fa, Fa,
(where 'a' is old) to produce an appropriate proof
procedure. Steen reads ' x¼Fx' as 'the most un-F-like thing' (Steen
1972, p162), which explains why F x¼Fx' as 'the most un-F-like thing' (Steen
1972, p162), which explains why F x¼Fx entails Fa, since if the most un-F-like
thing is in fact F, then the most plausible counter-example to
the generalisation is in fact not so, making the
generalisation exceptionless. But there is a more important
reason why the rule of universal quantifier elimination is
best broken up into two parts. x¼Fx entails Fa, since if the most un-F-like
thing is in fact F, then the most plausible counter-example to
the generalisation is in fact not so, making the
generalisation exceptionless. But there is a more important
reason why the rule of universal quantifier elimination is
best broken up into two parts.
For Jeffrey's rules only allow him 'limited upward
correctness' (Jeffrey 1967, p167), since Jeffrey has to say,
with respect to his universal quantifier elimination rule,
that the range of the quantification there be limited merely
to the universe of discourse of the path below. This is
because, if an initial sentence is false in a valuation so
also must be one of its conclusions. But the first epsilon
rule which replaces Jeffrey's rule ensures, instead, that
there is 'total upwards correctness'. For if it is false that
everything is F then, without any special interpretation of
the quantifier, one of the given consequences of the universal
statement is false, namely the immediate one -- since F x¼Fx is in fact equivalent to (x)Fx. A similar
improvement also arises with the existential quantifier
elimination rule. For Jeffrey can only get 'limited downwards
correctness', with his existential quantifier elimination rule
(Jeffrey 1967, p165), since it is not an entailment. In fact,
in order to show that if an initial sentence is true in a
valuation so is one of its conclusions, in this case, Jeffrey
has to stretch his notion of 'truth' to being true either in
the given valuation, or some nominal variant of it. x¼Fx is in fact equivalent to (x)Fx. A similar
improvement also arises with the existential quantifier
elimination rule. For Jeffrey can only get 'limited downwards
correctness', with his existential quantifier elimination rule
(Jeffrey 1967, p165), since it is not an entailment. In fact,
in order to show that if an initial sentence is true in a
valuation so is one of its conclusions, in this case, Jeffrey
has to stretch his notion of 'truth' to being true either in
the given valuation, or some nominal variant of it.
The epsilon rule which replaces Jeffrey's overcomes this
difficulty by not employing names, only demonstrative
descriptions, and by being, as a result, totally downward
correct. For if there is an F then that F is F, whatever name
is used to refer to it. The epsilon calculus terminology thus
precedes any naming: it gets hold of the more primitive,
demonstrative way we have of referring to objects, using
phrases like 'that F'. Thus in explication of the predicate
calculus rule we might well have said
suppose there is an F, well, call that F 'a', then Fa,
but that requires we understand 'that F' before we come to
use 'a'.
So how does the Second Epsilon Theorem follow? This
theorem, as before, states that an epsilon calculus proof of
an epsilon-free theorem may be replaced by a predicate
calculus proof of the same formula. But the transformation
required in the present setting is now evident: simply change
to new names all epsilon terms introduced in the epsilon
calculus quantifier elimination rules. This covers both the
new names in Jeffrey's first rule, but also the odd case where
there are no old names in Jeffrey's second rule. The epsilon
calculus proofs invariably use constant epsilon terms, and are
thus effectively in Leisenring's epsilon star system.
Epsilon terms which are non-constant, however, crucially
enter the proof of the First Epsilon Theorem. The First
Epsilon Theorem states that if C is a provable predicate
calculus formula, in prenex normal form, i.e. with all
quantifiers at the front, then a finite disjunction of
instances of C's matrix is provable in the epsilon calculus.
The crucial fact is that the epsilon calculus gives us access
to Herbrand functions, which arise when universal quantifiers
are eliminated from formulas using their epsilon definition.
Thus
( y)(x)¼Fyx, y)(x)¼Fyx,
for instance, is equivalent to
( y)¼Fy y)¼Fy x¼¼Fyx, x¼¼Fyx,
and so
( y)¼Fy y)¼Fy xFyx, xFyx,
and the resulting epsilon term ' xFyx' is a Herbrand function. xFyx' is a Herbrand function.
Using such reductions, all universal quantifiers can
evidently be removed from formulas in prenex normal form, and
the additional fact that, in a certain specific way, the
remaining existential quantifiers are disjunctions makes all
predicate calculus formulas equivalent to disjunctions.
Remember that a formula is provable if its negation is
reducible to absurdity, which means that its truth tree must
close. But, by K÷nig's Lemma, if there is no open path through
a truth tree then there is some finite stage at which there is
no open path, so, in the case above, for instance, if no
valuation makes the last formula's negation true, then the
tree of the instances of that negative statement must close in
a finite length. But the negative statement is the universal
formula
(y)Fy xFyx, xFyx,
by the rules of quantifier interchange, so a finite
conjunction of instances of the matrix of this universal
formula, namely Fyx, must reduce to absurdity. For the rules
of universal quantifier elimination only produce consequences
with the form of this matrix. By de Morgan's Laws, that makes
necessary a finite disjunction of instances of ¼Fyx. By
generalisation we thus get the First Epsilon Theorem.
The epsilon calculus, however, can take us further than the
First Epsilon Theorem. Indeed, one has to take care with the
impression this theorem may give that existential statements
are just equivalent to disjunctions. If that were the case,
then existential statements would be unlike individual
statements, saying not that one specified thing has a certain
property, but merely that one of a certain group of things has
a certain property. The group in question is normally called
the 'domain' of the quantification, and this, it seems, has to
be specified when setting out the semantics of quantifiers.
But study of the epsilon calculus shows that there is no need
for such 'domains', or indeed for such semantics. This is
because the example above, for instance, is also equivalent
to
¼Fa zFaz, zFaz,
where a =  y¼F y¼F xFyx. So the previous disjunction of instances
of ¼Fyx is in fact only true because this specific disjunct is
true. The First Epsilon Theorem, it must be remembered, does
not prove that an existential statement is equivalent to a
certain disjunction; it shows merely that an existential
statement is provable if and only if a certain disjunction is
provable. And what is also provable, in such a case, is a
statement merely about one object. Indeed the existential
statement is provably equivalent to it. It is this fact which
supports the epsilon definition of the quantifiers; and it is
what permits anaphoric reference to the same object by means
of the same epsilon term. An existential statement is thus
just another statement about an individual -- merely a
nameless one. xFyx. So the previous disjunction of instances
of ¼Fyx is in fact only true because this specific disjunct is
true. The First Epsilon Theorem, it must be remembered, does
not prove that an existential statement is equivalent to a
certain disjunction; it shows merely that an existential
statement is provable if and only if a certain disjunction is
provable. And what is also provable, in such a case, is a
statement merely about one object. Indeed the existential
statement is provably equivalent to it. It is this fact which
supports the epsilon definition of the quantifiers; and it is
what permits anaphoric reference to the same object by means
of the same epsilon term. An existential statement is thus
just another statement about an individual -- merely a
nameless one.
The reverse point goes for the universal quantifier: a
universal statement is not the conjunction of its instances,
even though it implies them. A generalisation is simply
equivalent to one of its instances -- to the one involving the
prime putative exception to it, as we have seen. Not being
able to specify that prime putative exception leaves Jeffrey
saying that if a generalisation is false then one of its
instances is false without any way of ensuring that that
instance has been drawn as a conclusion below it in the truth
tree except by limiting the interpretation of the
generalisation just to the universe of discourse of the path.
It thus seems necessary, within the predicate calculus, that
there be a 'model' for the quantifiers which restricts them to
a certain 'domain', which means that they do not necessarily
range over everything. But in the epsilon calculus the
quantifiers do, invariably, range over everything, and so
there is no need to specify their range.
7.
Sources
Ackermann, W. 1937-8, 'Mengentheoretische Begr³ndung der
Logik', Mathematische Annalen, 115, 1-22.
Asser, G. 1957, 'Theorie der Logischen Auswahlfunktionen',
Zeitschrift f³r Mathematische Logik und Grundlagen der
Mathematik, 3, 30-68.
Bernays, P. 1958, Axiomatic Set Theory, North
Holland, Dordrecht.
Bertolet, R. 1980, 'The Semantic Significance of
Donnellan's Distinction', Philosophical Studies, 37,
281-288.
Bourbaki, N. 1954, ╔lķments de Mathķmatique,
Hermann, Paris.
Bunt, H.C. 1985, Mass Terms and Model-Theoretic
Semantics, C.U.P., Cambridge.
Church, A. 1940, 'A Formulation of the Simple Theory of
Types', Journal of Symbolic Logic, 5, 56-68.
Copi, I. 1973, Symbolic Logic, 4th ed. Macmillan,
New York.
Devitt, M. 1974, 'Singular Terms', The Journal of
Philosophy, 71, 183-205.
Donnellan, K. 1966, 'Reference and Definite Descriptions',
Philosophical Review, 75, 281-304.
Egli, U. and von Heusinger, K. 1995, 'The Epsilon Operator
and E-Type Pronouns' in U. Egli et al. (eds.), Lexical
Knowledge in the Organisation of Language, Benjamins,
Amsterdam.
Evans, G. 1977, 'Pronouns, Quantifiers and Relative
Clauses', Canadian Journal of Philosophy, 7, 467-536.
Geach, P.T. 1962, Reference and Generality, Cornell
University Press, Ithaca.
Geach, P.T. 1967, 'Intentional Identity', The Journal
of Philosophy, 64, 627-632.
Goddard, L. and Routley, R. 1973, The Logic of
Significance and Context, Scottish Academic Press,
Aberdeen.
G÷del, K. 1969, 'An Interpretation of the Intuitionistic
Sentential Calculus', in J. Hintikka (ed.), The Philosophy
of Mathematics, O.U.P. Oxford.
Hazen, A. 1987, 'Natural Deduction and Hilbert's  -operator', Journal of Philosophical
Logic, 16, 411-421. -operator', Journal of Philosophical
Logic, 16, 411-421.
Hermes, H. 1965, Eine Termlogik mit
Auswahloperator, Springer Verlag, Berlin.
Hilbert, D. 1923, 'Die Logischen Grundlagen der
Mathematik', Mathematische Annalen, 88, 151-165.
Hilbert, D. 1925, 'On the Infinite' in J. van Heijenhoort
(ed.), From Frege to G÷del, Harvard University Press,
Cambridge MA.
Hilbert, D. and Bernays, P. 1970, Grundlagen der
Mathematik, 2nd ed., Springer, Berlin.
Hughes, G.E. and Cresswell, M.J. 1968, An Introduction
to Modal Logic, Methuen, London.
Jeffrey, R. 1967, Formal Logic: Its Scope and
Limits, 1st Ed. McGraw-Hill, New York.
Kalish, D. and Montague, R. 1964, Logic: Techniques of
Formal Reasoning, Harcourt, Brace and World, Inc, New
York.
Kneebone, G.T. 1963, Mathematical Logic and the
Foundations of Mathematics, Van Nostrand, Dordrecht.
Leisenring, A.C. 1969, Mathematical Logic and Hilbert's
 -symbol, Macdonald, London. -symbol, Macdonald, London.
Marciszewski, W. 1981, Dictionary of Logic,
Martinus Nijhoff, The Hague.
Meyer Viol, W.P.M. 1995, Instantial Logic, ILLC
Dissertation Series 1995-11, Amsterdam.
Montague, R. 1963, 'Syntactical Treatments of Modality,
with Corollaries on Reflection Principles and Finite
Axiomatisability', Acta Philosophica Fennica, 16,
155-167.
Neale, S. 1990, Descriptions, MIT Press, Cambridge
MA.
Priest, G.G. 1984, 'Semantic Closure', Studia
Logica, XLIII 1/2, 117-129.
Prior, A.N., 1971, Objects of Thought, O.U.P.
Oxford.
Purdy, W.C. 1994, 'A Variable-Free Logic for Anaphora' in
P. Humphreys (ed.) Patrick Suppes: Scientific
Philosopher, Vol 3, Kluwer, Dordrecht, 41-70.
Quine, W.V.O. 1960, Word and Object, Wiley, New
York.
Rasiowa, H. 1956, 'On the  -theorems', Fundamenta Mathematicae,
43, 156-165. -theorems', Fundamenta Mathematicae,
43, 156-165.
Rosser, J. B. 1953, Logic for Mathematicians,
McGraw-Hill, New York.
Routley, R. 1969, 'A Simple Natural Deduction System',
Logique et Analyse, 12, 129-152.
Routley, R. 1977, 'Choice and Descriptions in Enriched
Intensional Languages II, and III', in E. Morscher, J.
Czermak, and P. Weingartner (eds), Problems in Logic and
Ontology, Akademische Druck und Velagsanstalt, Graz.
Routley, R. 1980, Exploring Meinong's Jungle,
Departmental Monograph #3, Philosophy Department, R.S.S.S.,
A.N.U. Canberra.
Routley, R., Meyer, R. and Goddard, L. 1974, 'Choice and
Descriptions in Enriched Intensional Languages I', Journal
of Philosophical Logic, 3, 291-316.
Russell, B. 1905, 'On Denoting' Mind, 14, 479-493.
Sayward, C. 1987, 'Prior's Theory of Truth'
Analysis, 47, 83-87.
Slater, B.H. 1986(a), 'E-type Pronouns and  -terms', Canadian Journal of
Philosophy, 16, 27-38. -terms', Canadian Journal of
Philosophy, 16, 27-38.
Slater, B.H. 1986(b), 'Prior's Analytic', Analysis,
46, 76-81.
Slater, B.H. 1988(a), 'Intensional Identities', Logique
et Analyse, 121-2, 93-107.
Slater, B.H. 1988(b), 'Hilbertian Reference', No¹s,
22, 283-97.
Slater, B.H. 1989(a), 'Modal Semantics', Logique et
Analyse, 127-8, 195-209.
Slater, B.H. 1990, 'Using Hilbert's Calculus', Logique
et Analyse, 129-130, 45-67.
Slater, B.H. 1992(a), 'Routley's Formulation of
Transparency', History and Philosophy of Logic, 13,
215-24.
Slater, B.H. 1994(a), 'The Epsilon Calculus' Problematic',
Philosophical Papers, XXIII, 217-42.
Steen, S.W.P. 1972, Mathematical Logic, C.U.P.
Cambridge.
Thomason, R. 1977, 'Indirect Discourse is not
Quotational', Monist, 60, 340-354.
Thomason, R. 1980, 'A Note on Syntactical Treatments of
Modality', Synthese, 44, 391-395.
Thomason, R.H. and Stalnaker, R.C. 1968, 'Modality and
Reference', No¹s, 2, 359-372.
|

