Кнут Дональд Э. **

АЛГОРИТМИЧЕСКОЕ МЫШЛЕНИЕ И МАТЕМАТИЧЕСКОЕ МЫШЛЕНИЕ

Перев. Лебедева. И.В.

Моя задача в настоящей статье — в вызвать обсуждение философской проблемы, которая давно меня занимает: какова истинная роль понятия "алгоритм" в математических науках?

Многие годы я остаюсь при мнении, что прикладная математика, в первую очередь — изучение алгоритмов. Не все мои коллеги со мной соглашаются, но выясняется, что источник нашего несогласия в том, что мое понимание алгоритмов намного шире: я склонен считать, что алгоритмы охватывают весь круг понятий, использующих детерминированные процессы, включающие структуру данных, которыми оперируют, как и структуру последовательности выполняемых операций; иные рассматривают алгоритмы лишь как разнообразные методы решения конкретных задач, аналогичные отдельным теоремам математики.

В США то, что делают мои коллеги и я, называется computer science; так подчеркивается то, что алгоритмы исполняются машинами. Живи я в Германии или Франции, область, в которой я работаю, называлась бы Informatik или informatique, что выделяло бы то, над чем работают алгоритмы скорее, чем сами процессы. В Советском Союзе та же область сейчас известна или как кибернетика — подчеркивается контроль над процессами — или как прикладная математика — выделяется полезность изучаемого и его связь с математикой вообще. Я полагаю, что название нашей области — не вопрос жизненной важности, коль скоро мы будем продолжать то, что делаем, независимо от того, как это называется. В конце концов, другие науки, как то: математика или химия – уже не слишком связаны с этимологией своих названий. Тем не менее, если б у меня была возможность голосовать за название собственной науки, я предпочел назвать ее алгоритмикой — словом, придуманным Дж. Ф. Траубом [12] примерно 20 лет назад.

Возможность участвовать в таком симпозиуме особенно сконцентрировала будоражившие меня вопросы. Было самое время подумать о долгосрочных проблемах, размышлять о которых я редко мог позволить себе из-за безумного темпа моей деятельности дома. Место проведения симпозиума, его богатая история и грандиозный пейзаж подвигли меня на то, чтобы не только взглянуть на корни своих занятий — но также и вперед, пытаясь уяснить суть моей работы. С возобновляющейся настойчивостью спрашивал я себя: Каково отношение алгоритмов к современной математике? Существует ли некое существенное различие между алгоритмической точкой зрения и традиционным математическим мировоззрением? Верно ли, что у 6ольшинства математиков существенно иной мыслительный процесс, чем у специалистов по прикладной математике? Почему среди университетских математиков логики и, в меньшей степени, комбинаторщики, склонны проявлять больший интерес к программированию, чем их коллеги?

В каком-то смысле я думал над такими вопросами со студенческих времен. Я стал изучать высшую математику в 1957 году и в том же году начал работать с цифровыми компьютерами, но до 1961 года я никаким нетривиальным образом не смешивал свое математическое мышление с мышлением программиста. В одном здании я был математиком, в другом — программистом, словно у меня было раздвоение личности. В течение 1961 года меня волновала мысль о том, что у математики и кибернетики, возможно, есть общая основа, поскольку запись формы Бэкуса-Наура выглядела математично; итак, я купил книгу Хомского "Синтаксические структуры" и принялся искать алгоритм решения проблемы неоднозначности контекстно-свободных грамматик (не зная, что невозможность этого была доказана Бар-Хиллелом, Перлсом и Шамиром в 1960 году). Не стоит упоминать, что мне не удалось решить этой задачи, хотя я и нашел некоторые полезные необходимые и достаточные условия неоднозначности и, кроме того, вывел несколько других результатов, наподобие регулярности контекстно-свободных грамматик с одной переменной. Вот, думал я, отличная математическая теория, которую я был способен развить силой своей программистской интуиции; любопытно! Летом 1962 года я провел пару дней, анализируя хеширование с помощью линейного приближения, но это в действительности не выглядело соединением моего математического "я" с "я" программистским: это было лишь приложением комбинаторики к задаче, имеющей отношение к программированию.

Во время моей поездки в университет штата Иллинойс в 1979 году я встретил Джерри Де Янга, психолога с интересами в области компьютеров, который незадолго до того поставил интересный эксперимент с двумя группами студентов, посещавших вводные курсы по программированию. Группа 1 состояла из 135 студентов, намеревавшихся специализироваться в области программирования, в то время как группа 2 состояла из 35 учащихся, специализировавшихся по общественным наукам. Оба курса делали акцент на нечисленном программировании и различных структурах данных и контроля, хотя численные проблемы также изучались. Де Янг раздал вопросник, оценивающий так называемые "количественные способности" каждого студента, аналогичный тем, которые, видимо, оценивают математические способности, а также попросил их оценить их собственные успехи в классе. Впоследствии он узнал оценки, полученные студентами на самом деле, так что у него было три вида данных на. каждого студента.

В обоих случаях В хорошо коррелировало с С (коэффициент был около 0.6), так что мы можем заключить, что оценки преподавателя не были случайными и что эти показатели в некоторой степени обоснованы. Интересным было то, что у занимающихся программированием (группа 1) не было корреляции между А и В или А и С, в то время как била выразительная корреляция (примерно в 0.4) между соответствующими цифрами у студентов группы 2. Неясно, как интерпретировать эти данные, поскольку они укладываются в различные гипотезы; возможно, психологи умеют измерять такие способности только тех людей, которые мыслят, как психологи. Как бы то ни было, отсутствие корреляции между "количественными способностями" и успехами в программировании в первой группе вызывает во мне те чувства, которые я часто испытываю из-за различия между математическим и алгоритмическим мышлением.

Я посмотрел собрание показательных работ под названием "Математика: ее содержание, методы и значение" [1] и перечел сказанное А.Д. Александровым в его превосходном вступительном очерке (довольно интересно, что он со значением упоминает об аль-Хорезми). Александров перечислил черты, характеризующие математику:

С точки зрений вычислительной математики, понятие "типов мышления" не столь туманно, как раньше, ведь сейчас мы можем представить себе попытку заставить программу самостоятельно открыть математику. Какие же возможности мы должны заложить в этот искусственно созданный мозг, чтобы он смог достичь результатов, содержащихся на сотой странице выбранных книг?

Для того чтобы эксперимент был чистым, я придерживался следующих основных правил: ( 1} Все книги должны быть выбраны прежде, чем я загляну в какую-то из них. (2) В каждом случае необходимо изучить сотую страницу, поскольку я не знал a priori, что же именно на ней ни в одной из книг. Если вдруг окажется, что выбор сотой страницы неудачен, я не стану предпринимать попыток выбрать какой-то другой номер, чтобы получить результаты, более похожие на мои прогнозы. (3) Я не буду игнорировать никаких результатов, каждая избранная книга обязательно попадет в конечную выборку, так что я не буду поддаваться никаким предрассудкам.

Книга 1. "Анализ" Томаса. Сначала я взял ту самую книгу, которая когда-то познакомила меня с высшей математикой, учебник по анализу Джорджа Б. Томаса [11], по которой я учился на первом курсе. На странице 100 он решает следующую задачу: Какое значение x минимизирует время пути от точки (0,а) до точки (x,0) и далее до (d,-b), если вы движетесь со скоростью s₁ от (0,а) до (x, 0) и с некоторой другой скоростью s₂ от (x, 0) до (d,-b)?

Иными словами, мы хотим минимизировать функцию

Чтобы решить задачу, надо продифференцировать f(x). Получаем:

В то время как x пробегает значения от 0 до d, значение (sin θ₁)/s₁ растет, начиная с нуля, а значение (sin θ₂)/s₂ убывает до нуля. Следовательно, производная отрицательна на одном конце и положительна на другом; значит, существует точка, в которой она обращается в ноль, т.е. (sin θ₁)/s₁ = (sin θ₂)/s₂ и именно там достигается минимум. Томас отмечает, что это так называемый "закон Снелла" в оптике; лучи света откуда-то знают наикратчайший путь.

Книга 2. Обзор математики. Возвращаясь к обзорным томам под редакцией Александрова и др. [1], мы выясняемы, что сотая страница входит в главу по анализу Лаврентьева и Никольского. Она дает красивый способ вычисления производной функции log _a х:

Логарифм — непрерывная функция, следовательно, имеем:

,

так как было доказано, что когда п стремиться к бесконечности, как по целым, так и по дробным значениям, величина (1 + 1/n) стремится к константе, обозначаемой е. Здесь доказательство содержит операции с формулами и требует знания предела.

Книга 3. Общая топология Келли. Третьей из выбранных книг был стандартный курс топологии [4], где на странице 100 было следующее упражнение: “Задача А. Образ связного множества при непрерывном отображении связен.” Решения не приводится, хотя я могу предположить, что подразумевалось нечто в таком роде. Сначала мы вспоминаем необходимые определения: функция f из топологического пространства Х в топологическое пространство Y непрерывна, когда при обратном отображении образ f ^-1(V) открыт в Х для любого открытого множества V из Y, топологическое пространство Х связно в том случае, когда оно не может быть представлено в виде объединения двух непустых открытых непересекающихся подмножеств. Поэтому давайте попытаемся доказать, что Y связно, предполагая, что f непрерывна, а Х связно, где f(X) =Y. Если Y=V₁ U V₂, где V₁ и V₂ непересекающиеся открытые множества, то тогда Х = f ^–1(V₁) U f ^–1(V₂), где f ^–1(V₁) и f ^–1(V₂) не пересекаются и открыты. Отсюда следует, что или f ^–1(V₁), или f ^–1(V₂) пусто; пусть пусто f ^–1(V₁). Окончательно, из всего сказанного получаем, что V₁ пусто, так как V₁с f( f ^–1(V₁)), что и требовалось доказать.

Логика рассуждений в этом случае немного отличается от того, что мы видели в предыдущих примерах; в основном доказательство состоит из последовательности логических переходов от исходной гипотезы к требуемому результату, используя всевозможные выражения типа “f ^–1(A∩B) = f ^–1(A) ∩ f ^–1(B)”. Это аналогично тому, как мы строим цепочку команд для ЭВМ, преобразующих входные данные в выходные, используя разнообразные подпрограммы, хотя в топологии результаты гораздо более абстрактны.

И еще один тип математического мышления использован в этом случае, и нам нельзя про это забывать: кто-то должен был определить понятия непрерывности и связности так, чтобы это привело к построению глубокой теории, имеющей множество приложений, обобщая таким образом множество отдельных фактов, доказанных еще до того, как была воспринята абстракция.

Книга 4. Пример из 18 века. Очередная книга из моего списка была собранием математических первоисточников Стройка, в которой цитируются статьи знаменитых авторов, живших в 1200-3800 г.г. н.э. Сотая страница посвящена попыткам Эйлера доказать основную теорему алгебры, в процессе чего он получил следующий вспомогательный результат: “Теорема4. Каждый полипом четвертой степени x⁴ + Ах³ + Вх² + Сх + D с действительными коэффициентами может быть разложен на два квадратичных.”

Вот как он это доказывает. Сначала он сводит задачу к случаю А=0, полагая х = y - A/4. Он приходит к необходимости разрешить (х²+их+ α)(x² -их+ β) = υ⁴+ Вх² + Сх + D для u, α и β, т.е. найти решение уравнений В = а + β – θ², С = (β - а)и, D = αβ. Эти уравнения приводят к следующим отношениям 2β = Β+ u²+ С/и, 2α = В + u²— С/и и (B + u²)² – C²/u²= 4D. Но кубический многочлен (u²)³ + 2B(u²)² + (B² – 4D)u² – C² пробегает значения от –C² до ∞, когда u² изменяется от 0 до ∞, то есть обязательно существует положительный корень, и разложение получено.

(Эйлер приходит к обобщению, утверждая, что каждый полином ступени 2ⁿ может быть разложен на два степени 2^n-1 через тот факт, что полином нечетной степени относительно и² имеет отрицательный свободный член. Но эта часть его рассуждений не была строгой; позже Лагранж и Гаусс указали на значительный пробел.)

Когда я впервые увидел этот пример, мне показалось, что он гораздо более "алгоритмичен", чем предыдущие, — возможно потому, что Эйлер главным образом объясняет, как, взяв за исходные данные полином четвертой степени, получить на выходе два квадратичных. Характеристики вход/выход — важный аспект алгоритма; однако данная конструкция Эйлера достаточно проста и прямолинейна, так что она не демонстрирует сложных структур контроля, какие обычно бывают в алгоритмах. Типы рассуждения, которые здесь можно выделить, вероятно, такие: (а) свести общий случай к более простому частному (показывая, что А можно считать равным нулю, и замечая, что получающееся уравнение шестой степени относительно и — на самом деле уравнение третьей степени для и²), (b) операции с формулами для решения системы уравнений с неизвестными а, β и и; (c) обобщение, распознавание образца, примененного для уравнения четвертой степени, который, видимо, распространяется на уравнения 8, 16 и т.д. степеней.

Книга 5. Абстрактная алгебра. Следующей из выбранных книг был еще один стандартный учебник: "Коммутативная алгебра" Зарисского и Самюэля [14]. Их сотая страница посвящена обшей структуре произвольных полей. Пусть k и К – поля, и k С К; степень трансцендентности К над k определяется как мощность любого "базиса трансцендентности" L в К над k, а именно любого такого множества L, что все его конечные подмножества алгебраически независимы над k и любой элемент из К алгебраичен над k(L), т.е. является корнем многочлена с коэффициентами из минимального поля, содержащего k U L. В ходе изложения обнаруживается, что эта мощность – корректно определенный инвариант для k и К, т.е. все базисы трансцендентности в К над k имеют одну и ту же мощность.

И вот Теорема 26. Если k С К С Κ, то степень трансцендентности Κ на k равна сумме степеней трансцендентности К над k и Κ над К. Для доказательства этой теоремы Зарисский и Самюэль полагают, что L — базис трансцендентности К лад k и L — базис трансцендентности Κ над К; идея заключается в том, чтобы доказать, что L U L — базис трансцендентности в Κ над k и требуемый результат следует из того, что L и L не пересекаются.

Предлагаемое доказательство достаточно несложно, и его стоит изучить подробно. Пусть {x₁, . . ., x_m, Х₁, . . ., Х_m} — конечное подмножество элементов из L U L, где x-ы — элементы из L, а X-ы —из L, и пусть они удовлетворяют уравнению над k, а именно:

,

где все α(ε₁,...,е_m,E₁,...,Е_M) — лежат в k и лишь конечное число элементов а ненулевые. Это уравнение можно переписать в виде

,

многочлен относительно Х с коэффициентами из К; отсюда следует, что все коэффициенты равны нулю, в силу алгебраической независимости L над К. Эти коэффициенты в свою очередь — многочлены над х с коэффициентами из k, поэтому все α должны равняться нулю. Иными словами, любое конечное подмножество из L U L алгебраически независимо.

Наконец, все элементы из К алгебраичны над k(L) и все элементы из Κ, алгебраичны над К(L). Из ранее построенной теории алгебраических расширений следует, что все элементы из Κ алгебраичны над k(L)(L), наименьшим полем, содержащим k U L U L. Отсюда следует, что L U L удовлетворяет всем условиям базиса трансцендентности.

Отметим, что в доказательстве использованы довольно изощренные "структуры данных", т.е. оно содержит сложные объекты, в данном случае многочлены многих переменных. Ключевая идея состоит в трюке, основанном на эквивалентности многочленов над k в (*) и многочленов над k(L) в (**). В действительности, структурная теория поля, описанная в этой части книги Зарисского и Самюэля, по существу — теория о структурах данных, с помощью которой можно представить все элементы поля и оперировать ими. Теорема 26 не столь важна по сравнению с построением базиса трансцендентности, который появляется в доказательстве.

Книга 6. Метаматематика. Я выбрал "Введение в метаматематику" Клини [6] как типичную книгу по логике. На странице 100 говорится об "устранении дизъюнкций". Предположим нам дано (1) ├ A \/ В, (2) А ├ С и (3) В ├ С. Далее, с помощью только что доказанного правила (2) и (3) дают:

Из (1) и (4) мы можем заключить “(5) ├ С”. Клини подчеркивает, что это известная идея перебора вариантов. Если или А, или В верно, то мы можем в первом случае предположить, что А верно (тогда С выполняется), или во втором случае В верно (и тогда С опять выполняется). Отсюда следует, что С верно в любом случае.

Я надеялся затронуть здесь более принципиальный метаматематический аргумент, что-нибудь, типа "все, что может быть доказано в системе X, может быть доказано в системе Y", так как такие аргументы часто по существу — алгоритмы, которые переводят произвольное X-доказательство в Y-доказательство. Но страница 100 оказалась более элементарной: это всего лишь вводная книга.

Книга 7. Кнут. А моя собственная книга [6] алгоритмична? Ну, сотая страница, в частности, не особенно, так как она является частью введения в математические методы, которые появляются прежде, чем я углубляюсь в настоящую суть программирования. Проблемы, обсуждаемые на этой странице - получить математическое ожидание и стандартное отклонение числа "орлов" в n подбрасываниях монеты, когда каждое независимое испытание выдает "орел" с вероятностью p и "решку" с вероятностью q = 1- р. Я ввожу величину р_nk для вероятности того, что "орел" выпадет k раз и замечаю

.

и получаю G_n(z) = (q+pz)G_n-1(z), G₁(z) = q+pz. Отсюда G_n(z) = (q+pz)ⁿ и

mean(G_n) = nmean(G₁) = pn; var(G_n) = nvar(G₁) = pqn.

.

к 2ne^iq - kк ² = 4n² +k² –4nkcosq = (2n - k)² + 4nk(1 - cosq ) = (2n - k)² + 8nksin^2q /2.

Замена q на дает возможность переписать интеграл в виде

,

где f_n(x) = 0 для и отсюда

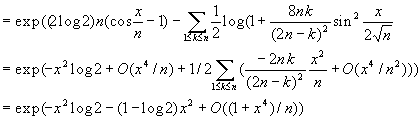
Таким образом, f_n(x) равномерно сходится к на любом конечном интервале. Более того, мы имеем и

для

так как косинус "свернут" с помощью своего ряда Маклорена; следовательно, к f_n(x)к при всех п меньше, чем интегрируемая функция , где с = 1 — p ²/12. В равномерно ограниченной последовательности законен внос предела под знак интеграла:

.

Эти преобразования дают некоторое представление о том , как далеко ушла математика со времен аль-Хорезми до 1920 года. Оно включает операции с формулами и здание ассимптотики поведения функций одновременно с подбором подходящей функции f_n, которая позволяет строго провести замену

0пределение fn(x) требует четкого понимания поведения функций типа ехр x и соs x.

Сотая страница книги Бишопа содержит следствие 3 из теоремы Стоуна-Вейерштрасса, доказанной на предыдущих страницах. Любую равномерно непрерывную функцию на компактном множестве Х М R можно с любой точностью приблизить многочленами над R. И вот доказательство: "Из леммы 5: функция х → │х— хо │ может быть приближена на Х с любой точностью. Тогда теорема следует из следствия 2".

Мы могли бы назвать это компактным доказательством! Прежде чем развернуть его, объясняя, что такое лемма 5 и следствие 2, я хотел бы подчеркнуть, что это доказательство по сути — алгоритм; алгоритм, который берет как входные данные произвольный конструктивно определенный компакт X, непрерывную функцию f и точность e и выдает многочлен, приближающий f с точностью e во всех точках X. Более того, он оперирует с алгоритмами, ведь f задается алгоритмом особого типа и действительные числа по существу — тоже алгоритм.

Я постараюсь облачить неявный алгоритм Бишопа в явную форму языка Паскаль, хотя возможности современных языков программирования должны быть значительно расширены, чтобы отразить его конструкцию. Сначала рассмотрим лемму 5, которая утверждает, что для любого e > 0 существует многочлен r : R® R, такой что r (0) = 0 и

к к xк - r (x)к Ј e для любого к xк Ј 1. Доказательство Бишопа, которое превращает лемму в алгоритм, по сути такое:

function Лемма5 (e : действит.): R – полином.;

var N: целое; g, p: R – полином.;

begin N: = подходящая функция от e ;

Здесь количество узлов N надо взять достаточно большим, чтобы получить к g(t) – (1-t)^{1/2к Ј} e /2 для 0 Ј t Ј 1.

Еще одна пропущенная часть доказательства. на странице 100 — следствие 2, которое утверждает, что если Х — произвольное компактное метрические пространство и G — множество всех функций х → r (х, x₀), где х_0О Х и r (х, y) обозначает метрическое расстояние от x до у, то "A(G) плотно в C(X)". Это значит, что все равномерно непрерывные действительнозначные функции в Х могут быть аппроксимированы с любой точностью функциями, полученными из G конечным числом операций сложения, умножения и умножения на действительные числа. Следствие 2 Бишопа оказывается ложным, когда Х содержит лишь одну точку, так как в этом случае G и A(G) состоят только из нулевой функции. (Я заметил этот пробел, когда пытался сформулировать, доказательство явно, в виде алгоритма.) Но погрешность легко исправить.

Для наших целей лучше всего переформулировать следствие 2 Бишопа в следующем виде: "Пусть Х —компактное метрическое пространство, содержащее, по крайней мере, две точки, и пусть G — множество всех функций вида х → сr (х, x₀) при с > 0 и х_0О Х. Тогда G — разделяющее семейство для X. Я повторю бишоповское определение разделяющего семейства через минуту; сначала я хотел бы упомянуть теорему 7, теорему Стоуна-Вейерштрасса, доказательство которой не буду разбирать подробно, а, именно тот факт, что А(G) плотно в C(X), когда G — разделяющее семейство равномерно непрерывных функций над компактным метрическим пространством X. С точки зрения этой теоремы, моя переформулировка следствия 2 влечет его в том виде, как оно приведено у Бишопа.

Разделяющее семейство – это набор действительнозначных функций G над X, вместе с функцией d , отображающей R⁺ в R⁺, а также два алгоритма выбора s и t . Алгоритм s берет в качестве входных данных произвольные элементы х, у из Х и положительное число e , где r (х, y) і e и выдает такой элемент g из G, что для любого z из Х имеем:

r (х, z) Ј d (e ) влечет п g(z)п Ј e ,

r (х, z) Ј d (e ) влечет п g(z) - 1п Ј e .

Алгоритм t берет как входные данные произвольный элемент у из X, такой что справедлива вторая из приведенных выше импликаций для всех zО X.

Итак, переформулированное следствие 2 – алгоритм, имеющий на входе нетривиальное компактное метрическое пространство и на выходе — разделяющее семейство (d ,s ,t ), в котором s и t выбирают функции вида r (х, x₀). Вот его построение:

function Следствие 2(X: компактное метрическое пространство;

{y₀ и y₁ — различные элементы X}

var d : function R⁺ ® R⁺;

d: function X ґ X ® R⁺;

s : function X ґ X ґ R^+® C(X);

t : function X ґ R^+® C(X);

begin d(x,y) : = Xr (х, y); {это функция метрики в X}

Мое обозначение сложных типов, используемое в этих алгоритмах, не самое удобное, но я надеюсь, что оно достаточно легло воспринимается без дальнейших объяснений. Правило выбора s , определяемое этим алгоритмом, обладает требуемыми свойствами, поскольку, например, при r (х, y) > e и r ( y, z) Ј d (e ) Ј e ² получаем, что п g(z) - 1п =п r (х, z) - r (х, y)п /r (х, y) Ј r ( y, z)/ r (х, y) Ј e .

Доказательство следствия 3, данное Бишопом, теперь может быть представлено более явно в виде алгоритма следующим образом. Если Х — компактное подмножество в R, то по определению Бишопа, мы можем вычислить М = bound (X) так, чтобы Х содержался в замкнутом отрезке [-М, М]. Предположим, что теорема 7 – процедура, чьи входные параметры состоят из компактного метрического пространства X, разделяющего семейства (d ,s ,t ) над X, которое выбирает функции из некоторого множества G М С(Х), равномерно непрерывной функции f: X® R и положительного числа e . Тогда на выходе у процедуры — элемент А из А(G), а именно конечная сумма, членов вида Сg₁(x). . . g_m(x) при т і 1 и каждое g_{i О} G; этот результат удовлетворяет к A(x) – f(x) к Ј e для всех x из X.

function Следствие 3 (X: вещественный компакт;

f - непрерывная на Х функция;

e : положит.): R - полином;

vаг р,q,r: R - полином; М,В: действит.; y₀, y₁: элемент X;

А: элемент А(G), где G — множество функций x ® ск х - х_0к

bеgin М := bоипd(Х);

if тривиально(Х) then r(t):= f(y₀)

else bеgin у₁ := элемент(X \ {y₀});

А := Теорема 7(Х, Следствие 2{Х, y₀, y₁), f, e /2)

p(t) := Лемма 5 (e /В);

Очевидно, было бы особенно интересно с точки зрения языков программирования высокого уровня найти элегантные обозначения, в которых конструкции Бишопа были бы понятными и явными.

Предварительные итоги. Что же именно мы получили из этих девяти случайно выбранных математических примеров? Перво-наперво, они подчеркнули нечто, что должно было быть очевидным с самого начала, а именно то, что не существует "математического мышления" как отдельного, изолированного понятия; математики используют множество различных способов мышления, а не только один. Мой вопрос о программистском мышлении как о чем-то отличном от математического, следовательно, должен быть переформулирован. Действительно, когда я вновь вспоминаю мои студенческие дни, я понимаю, что не носил только маску программиста во время занятий программированием и маску математика, когда посещал лекции, у меня также было множество масок, представляющих различные модели мышления, которыми я пользовался, когда редактировал студенческий журнал или когда был офицером братства и т.д..

Программисты, я думаю, заметят, что двух типов мышления не хватает в тех примерах, которые мы изучили; это, возможно, и отличает программиста от математика. Во-первых, почти нет понятия "сложности", или экономичности, действия. Математика Бишопа конструктивна, но в ней не хватает некоторых составных частей алгоритма, потому что она игнорирует так называемую "стоимость" конструкции. Если бы мы учли все детали теоремы Стоуна-Вейерштрасса по отношению к простым функциям, то, похоже, нам пришлось бы подняться до приближения многочленами степени, скажем, 10⁶, хотя подходящий многочлен шестой степени можно найти при помощи более эффективной схемы.

В наших девяти примерах нет ничего похожего на "n: = n+1", кроме как в рассуждениях Эйлера, которые по существу начинаются с присваивания x : = x - A/4. Эта операция присваивания у Бишопа на самом деле таковой не является, это просто определение величин, и эти определения нельзя изменить. Эта. несогласованность между классической математикой и программированием хорошо видна в том, что Берк, Голдстайн и фон Нейман не использовали понятия присвоения в своих ранних заметках по компьютерному программированию; вместо этого они использовали забавное понятие in-between (см. [7]).

Программисту, кажется, больше, чем традиционному математику, нравится общаться со множеством достаточно различных случаев. Структуры данных в вычислительной математике не должны быть однородными, алгоритм может содержать множество различных шагов. Иногда в этом и есть слабость программистов, потому что мы не стараемся изо всех сил добиться общности; но иногда это преимущество, так как мы можем спокойно обращаться с существенно неоднородными понятиями.

На симпозиуме в Ургенче я сбольшим удовольствием выслушал лекцию Г.С. Цейтина на эту тему; я настоятельно советую вам познакомиться с ней [13].

---

Список литературы:

[1] Математика: ее содержание, методы и значение, под ред. Александрова и др. (Акад. Наук СССР, 1956)

[2] Errett Bishop, Foundations of Constructive Analysis (N.Y.McGraw-Hill, 1967).

[3] Fred Gruenberger, "The role of education in preparing effective computing personnel", в "Effective vs. Efficient Computing" под ред. F. Gruenberger (Englewood Cliff, N.J.: Prentice-Hall, 1973), 112-120.

[4] Келли Дж. Общая топология (М., Наука, 1968). Перев. с англ. А.В. Архангельского.

[5] Клини Ст. Введение в метаматематику (М., Изд. Иностр. лит-ры, 1957). Перев. с англ. А. С. Есенина-Вольпина.

[6] Кнут Д. Искусство программирования для ЭВМ. Т1: Основные алгоритмы. (М., Мир, 1976). Перев. с англ. Г.П. Бабенко и Ю.М. Баяповского.

[7] Donald E. Knuth and Luis Trabb Pardo, "The early development of programming languages", Encyclopedia of Computer Science and Technology 7 (N.Y. Marcel Dekker, 1977), 419-493.

[8] Donald E. Knuth, "Algorithms in modern mathematics and computer science", Lecture Notes in Computer Science 122 (Berlin: Springer, 1981), 82-89.

[9] Пойа Д., Сеге Г. Задачи и теоремы из анализа. (М., Наука, 1978), Перев. с нем. Д.А. Райкова.

[10] Struik, ed., A Source Book in Mathematics, 1200-1800 (Cambridge, Mass.: Harvard University Press, 1969).

[11] George B. Thomas, Calculus and Analytical Geometry, 2nd. ed. (Cambridge, Mass.: Addison-Wesley, 1956).

[12] Трауб Дж. Ф. Итерационные методы решения уравнений. (М. Мир, 1985) Перев. с англ.

[13] G.S. Tseitin, "From logicism to proceduralism" (An autobiographical account), Lecture Notes in Computer Science 122 (Berlin: Springer, 1981), 390-396.

[14] Зарисский О., Самюэль П. Коммутативная алгебра 1 (М., Изд. иностр. лит-ры, 1963). Перев. с англ. О.П. Введенского.

 

---

** Дональд Э. Кнут, профессор математики Стэнфордского университета., хорошо известен как автор "Искусства программирования на ЭВМ", серии справочной литературы, которую он планирует окончить в течение двух следующих десятилетий. Его математическая новелла "Сюрреальные числа" используется для преподавания методологии научных исследований для студентов старших курсов. В течение нескольких последних лет он придумал новые методы набора. математических текстов, которые сейчас входят в широкое употребление. Эта статья — отрывок из беседы, опубликованной в [8]. Подготовка. оригинала. была осуществлена при поддержке Национального научного фонда, грант МСS72-03752 АО3 и частично при поддержке Officе оf Navаl Research, контракт N0014-76-С-0330. Это издание было осуществлено пря поддержке Национального научного фонда, грант МSС-83-00984. Большое количество людей, слишком большое для того, чтобы их перечислять, поделились своими идеями во время обсуждения тем, затронутых в этой статье.